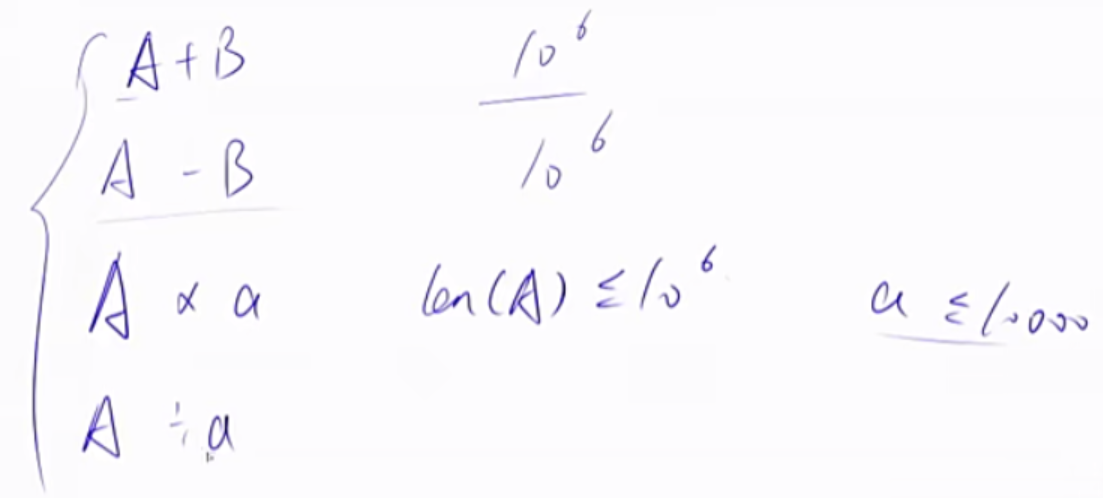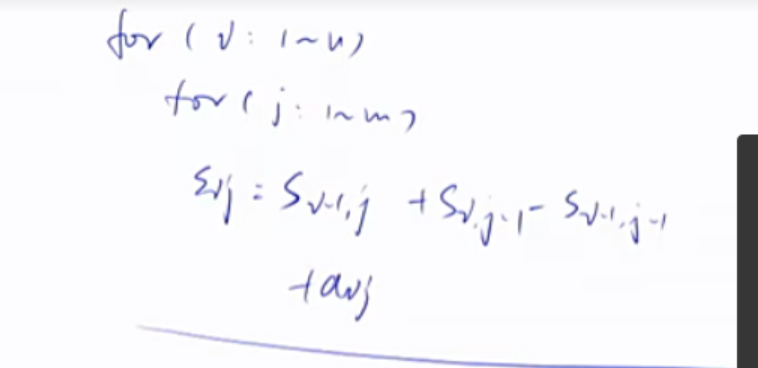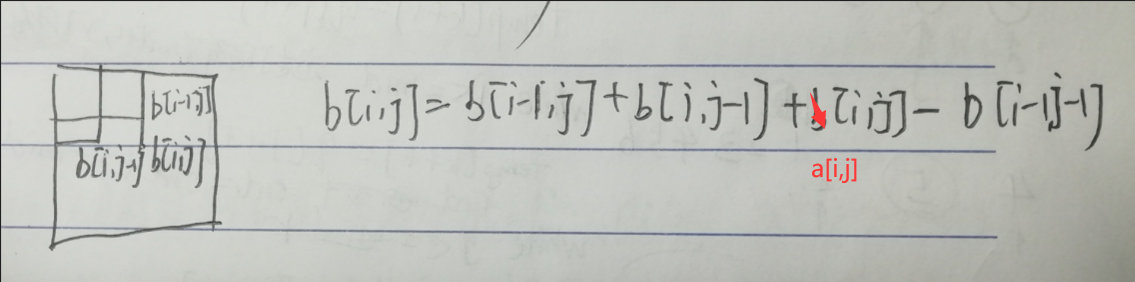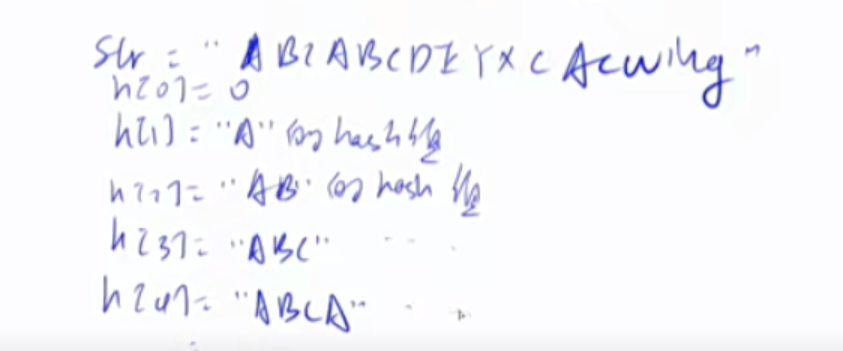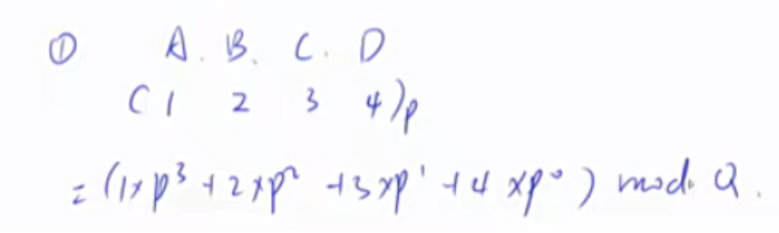Hexo
0%

AcWing算法学习

发表于 更新于 分类于
再次梳理算法模板

模板来源

快速排序

快速排序
快速排序
快速排序本身是不稳定的，但是可以采用\{data,index\}这样元组的形式，保证data相同的情况下，按照index先后顺序进行排序，就可以使得快速排序稳定。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void quick_sort(int q[], int l, int r)
{
    //如果区间里只有一个数或没有数，则直接返回
    if (l >= r) return;

    //i和j这样选的原因是，在循环中，我们总是i和j先向中间移动一格，然后再比较大小
    //一般不选第一个元素为x，因为有序数组复杂度会退化到n方
    int i = l - 1, j = r + 1, x = q[l + r >> 1];
    //x一定要是元素的值，不能是下标，如果是下标的话在下面交换的过程中值可能会改变
    while (i < j)
    {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        //如果两个指针还没有相遇，我们就交换
        if (i < j) swap(q[i], q[j]);
    }
    //注意相遇的情况是j在左边，i在右边
    //当写i-1，i时，x一定不能是q[l]，有可能会死循环，如[1,2]进行排序
    //同理，当写j，j+1的时候，x一定不能是q[r]
    //这里一定是和l和r有关，和mid没有任何关系
    quick_sort(q, l, j), quick_sort(q, j + 1, r);
}

快排模板
快排练习题

注意：
i==j的时候，意味着这个区间的x就位于区间中央。
i,j位置的意义是j左边（包括j)的元素都小于等于x，i右边（包括i）的元素都大于等于x。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include<iostream>
using namespace std;
int database[5000010];
int count = -1;
int aim = 0;
int n;

void quick_sort(int l,int r){
    if(l>=r) return;
    int i = l-1,j = r+1,x = database[i+j>>1];
    while(i<j){
        do {i++;}while(database[i]<x);
        do j--;while(database[j]>x);
        if(i<j) swap(database[i],database[j]);
    }
    int idx;
    if(j == aim&& (l+1==r||i == j)){
        count = database[aim];
        return;
    }
    else if(i == aim&& (l+1==r||i == j)){
        count = database[aim];
        return;
    }
    else if(i == j && aim>j){
        quick_sort(i+1,r);
    }
    else if(aim>j){
        quick_sort(i,r);
    }
    else{
        quick_sort(l,j);
    }
}
int main(){
    // freopen("data.in", "r",stdin);
    // freopen("BaoLi.out", "w", stdout);
    scanf("%d %d",&n,&aim);
    for(int i = 0;i<n;i++){
        scanf("%d",&database[i]);
    }
    quick_sort(0,n-1);
    if(count == -1){
        printf("%d",database[aim]);
    }else{
        printf("%d",count);
    }
    return 0;
}

归并排序

归并排序
归并排序
主要思想是分治。
递归的中界点是直接取区间中值。
快速排序的难点在于划分（把一个区间划分成两段），归并排序的难点在于合并，本质上是一个双指针算法。
为了维持归并排序的稳定，如果两个区间有相同的值，一般我们首选第一个区间。
归并排序的时间复杂度为O(nlogn)。每次合并的复杂度为O(n)，共有logn层。
归并排序
‘闭区间’写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
const int N = 1000010;
//归并排序需要一个辅助数组
int temp[N];
void merge_sort(int q[], int l, int r)
{
    //如果区间里面的元素个数是一个或是没有的话，直接返回
    if (l >= r) return;

    //确定分界点
    int mid = l + r >> 1;
    //递归排左边和右边区间
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);

    //k是记录temp数组中插入元素的位置指针
    //i，j指向左边和右边区间的起点
    int k = 0, i = l, j = mid + 1;
    //当两个区间内都还有数据的时候
    while (i <= mid && j <= r)
        //如果i指针指向的元素小于等于j指针指向的元素，那么把i指针的元素放入temp数组中
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        //否则就把j指针指向的元素放入temp数组中
        else tmp[k ++ ] = q[j ++ ];
    //如果left区间没有循环完，那么就将left剩余部分全部放入temp中
    while (i <= mid) tmp[k ++ ] = q[i ++ ];
    //如果right区间没有循环完，那么就将right剩余部分全部放入temp中
    while (j <= r) tmp[k ++ ] = q[j ++ ];

    //把结果放回到q数组中，注意i指针的起点为l，而j指针的起点为0
    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}

练习题目
教训：一定要开lld。
可以理解成状态转移，转移条件的关键在于cnt = cnt+mid-i+1这个式子。

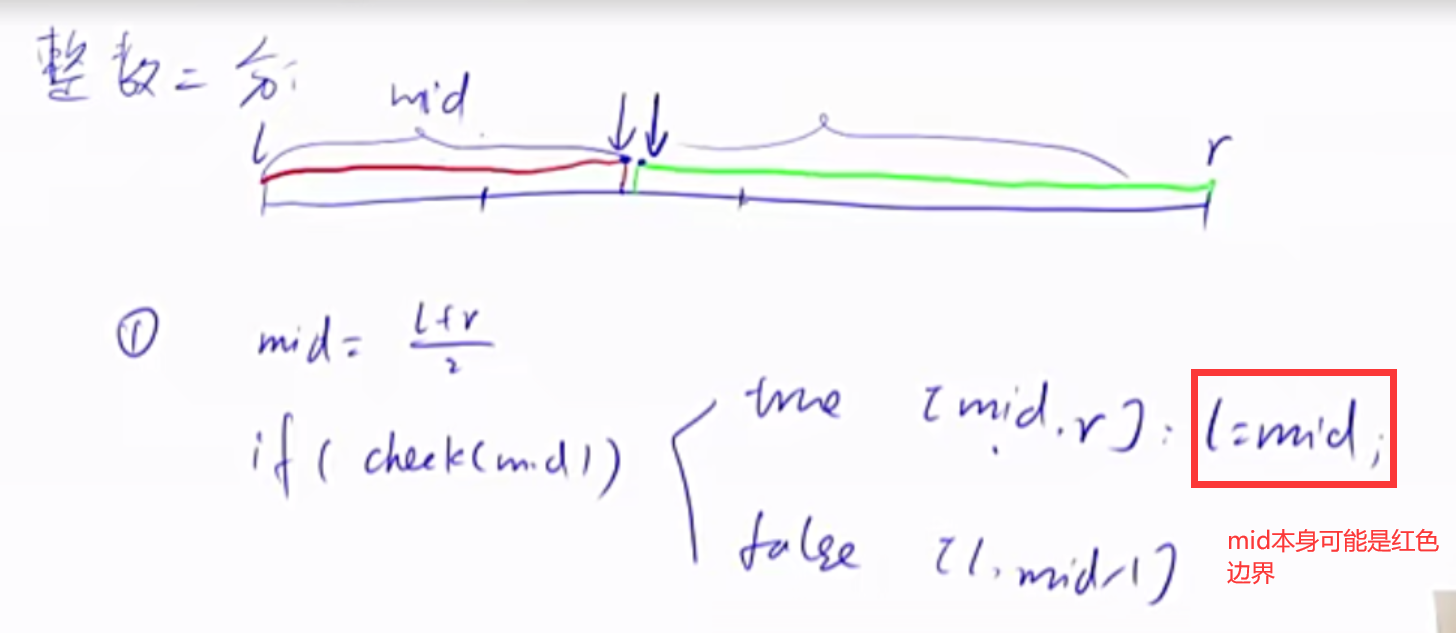
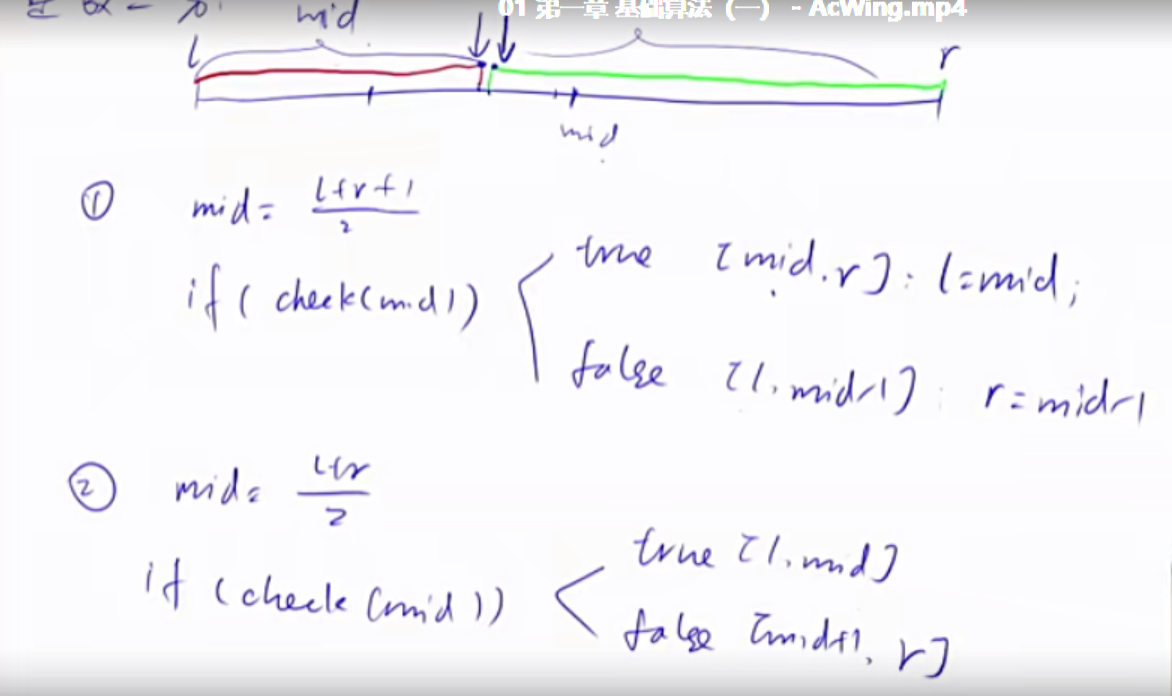
整数二分

整数二分有两个模板，在不同情况下使用，防止稍不留神写出死循环。
算法思路：假设目标值在闭区间[l,r]中，每次将区间长度缩小一半，当l=r时，我们就找到了目标值。
有单调性的区间，一定可以二分，但是可以二分的题目，不一定非得有单调性。
整数二分的实质：我们定义了一个性质，这个性质在左半边区间是不满足的，在右半边区间是满足的，因为是整数上的二分，所以左右两个区间不存在交点。那么二分算法就可以寻找这两个区间的边界，既可以寻找左边区间的边界，也可以寻找右边区间的边界。
整数二分
模板1可以二分确定红色区间的边界，模板2可以二分确定绿色区间的边界。
整数二分
上图对应模板二，图片中有一处错误，mid = (l+r+1)/2。例如当l = r-1时，如果mid没有+1，mid = （l+r）/2 = l。如果check返回条件是true，则下一个区间依然传入的是[l,r]，就会陷入死循环。
整数二分
两个模板的选择方法：看每次更新时，check条件为真的区间，是l = mid还是r = mid

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：(其更新操作是r = mid或l = mid+1，计算mid时不需要加1)
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：(注意这个模板中mid需要加1)
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

二分的本质是每次都要选择答案所在的区间进行下一步的处理。二分的算法一定是有解的，就是模板可以给出一个答案的，如果这个答案不符合题目要求，这个才是无解的，这是由题目给的区间中不存在相应答案导致的。
练习题目

新思路：结合map来去重。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
class Solution {
public:
    map<int,map<int,int>> ma;
    vector<int>datain;
    int mid_search(int l, int r, int aim) {
        if (datain[l] == aim) {
            return l;
        }
        else if (datain[r] == aim) {
            return r;
        }
        int mid = (l + r) / 2;
        while (r - l > 1) {
            mid = (l + r) / 2;
            if (datain[mid] >= aim) {
                r = mid;
            }
            else {
                l = mid + 1;
            }
        }
        if (datain[r] == aim) {
            return r;
        }
        else if (datain[l] == aim) {
            return l;
        }
        else {
            return -1;
        }
    }
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>>result;
        sort(nums.begin(), nums.end());
        datain = nums;
        int len = nums.size();
        for (int i = 0; i < len; i++) {
            for (int j = i + 1; j < len; j++) {
                int res = 0 - (nums[i] + nums[j]);
                if (j + 1 >= len) continue;
                int k = mid_search(j + 1, len - 1, res);
                if (k == -1) continue;
                int cnt = nums[i] * 100 + nums[j] * 10 + nums[k];
                if (ma[nums[i]][nums[j]] != 0) continue;
                ma[nums[i]][nums[j]] = nums[k];
                if (nums[i] == 0 && nums[j] == 0) {
                    ma[nums[i]][nums[j]] = 1;
                }
                result.push_back({ nums[i],nums[j],nums[k] });
            }
        }
        return result;
    }
};

浮点数二分

浮点数二分的实现中l和r赋的新值都是mid相同。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
bool check(double x) {/* ... */} // 检查x是否满足某种性质

double bsearch_3(double l, double r)
{
    const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求，四位小数-6，五位小数-7，六位小数-8
    //可以不用精度去控制迭代，而是直接循环100次，就是L/(2^100)
    while (r - l > eps)
    {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    //返回l和返回r都是一样的
    return l;
}

练习题目
注意的地方：如果区间内有两个零点，那么零点定理是无效的，所以要好好利用两个根之间差距大于等于1来建立一个循环，里面是浮点数二分。
浮点数二分的对象是每个长度为1的区间。

高精度加法

四种高精度运算
大整数存储是把一个大整数存储到数组里面去。具体方式见下，这是为了在做加法的时候，可以方便地在数组的最高位补上一位数。
高精度1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// C = A + B, A >= 0, B >= 0
//主程序输入采用字符串类型，然后再每一位抠出来放到vector中去(逆序)。在这个过程中，要注意减去'0'这个偏移量。也因此，在主函数中，我们输出结果需要倒着输出。
//函数中传参加上引用，为了提交效率。
vector<int> add(vector<int> &A, vector<int> &B)
{
    //保证A的size一定大于B的size
    if (A.size() < B.size()) return add(B, A);

    vector<int> C;
    //t是进位
    int t = 0;
    //从个位开始相加
    for (int i = 0; i < A.size(); i ++ )
    {
        //如果i没有超过A的范围，t就加上A[i]
        t += A[i];
        //如果i没有超过B的范围，t就加上B[i]
        if (i < B.size()) t += B[i];
        C.push_back(t % 10);
        //计算下一位的进位t
        t /= 10;
    }
    //如果最高位还有进位的话，我们就需要在C的末尾再加上一个1
    if (t) C.push_back(t);
    return C;
}

高精度减法

练习题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
// C = A - B, 满足A >= B, A >= 0, B >= 0,如果是负数的话，只需要在main函数中打一个标记记录正负，不需要把他放入到vector数组中。
vector<int> sub(vector<int> &A, vector<int> &B)
{
    //答案数组C
    vector<int> C;
    //A的size一定是大于等于B的size的（大小确定的）
    //注意循环的顺序
    for (int i = 0, t = 0; i < A.size(); i ++ )
    {
        t = A[i] - t;
        //如果在i位置B有这一位的话，那么就减去B。
        if (i < B.size()) t -= B[i];
        //如果t大于等于0，那么+10没用；如果t小于0，那么就模拟向高位借一的过程
        C.push_back((t + 10) % 10);
        //根据相减的结果判断是否向高位有借位
        if (t < 0) t = 1;
        else t = 0;
    }
    //如果C.size()>1，我们才可以去掉多余的0.如果是只有一位数且为0的话，我们不能去掉这个0，因为它表示我们最后的结果
    //去掉前导零，即003->3
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}
//判断A≥B
bool cmp(vector<int>&A,vector<int>&B){
    if(A.size()>B.size()){
        return A.size()>B.size();
    }
    for(int i = A.size()-1;i>=0;i--){
        if(A[i]!=B[i]){
            return A[i]>B[i];
        }
    }
}
int main(){
    if(cmp(A,B)){
        printf('-');
    }
}

高精度乘法

A以string类型读入，B以int类型读入。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// C = A * b, A >= 0, b >= 0
vector<int> mul(vector<int> &A, int b)
{
    vector<int> C;

    int t = 0;
    //当t中还有向更高位的进位时，不退出循环，将他push到C中。
    for (int i = 0; i < A.size() || t; i ++ )
    {
        //因为循环退出条件还可能使得i超过范围，所以需要判断一下
        if (i < A.size()) t += A[i] * b;
        C.push_back(t % 10);
        //低位的数放到高位的时候，权重就会少10
        t /= 10;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();

    return C;
}

高精度除法

练习题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// A / b = C ... r, A >= 0, b > 0
//余数是通过引用传过去的
vector<int> div(vector<int> &A, int b, int &r)
{
    vector<int> C;
    r = 0;
    //除法一定要从最高位除起
    for (int i = A.size() - 1; i >= 0; i -- )
    {
        //模拟在实际计算中，我们把下一位写在上一次除法余数的后面
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    //C中0存储的是最高位，但是在前面的高精度算法中，我们使用0存储最低位的，所以这里做一个逆向。
    //需要头文件algorithm
    reverse(C.begin(), C.end());
    //别忘记去掉前导零
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

一维前缀和

一维前缀和
1、注意定义S[0] = 0，方便处理边界，如1~10的元素和，为S[10]-S[0]。这样不需要对从1开始的前缀和进行特判，形式统一。
2、注意[l,r]区间内数的和的求法。
3、注意元素下标从1开始，这样才可以定义出来S[0]。
4、cin读入加速：ios::sync_with_stdio(false);其作用是使cin与标准输入输出不需要同步了。副作用是代码中不能使用scanf了。

1
2
S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]

练习题目

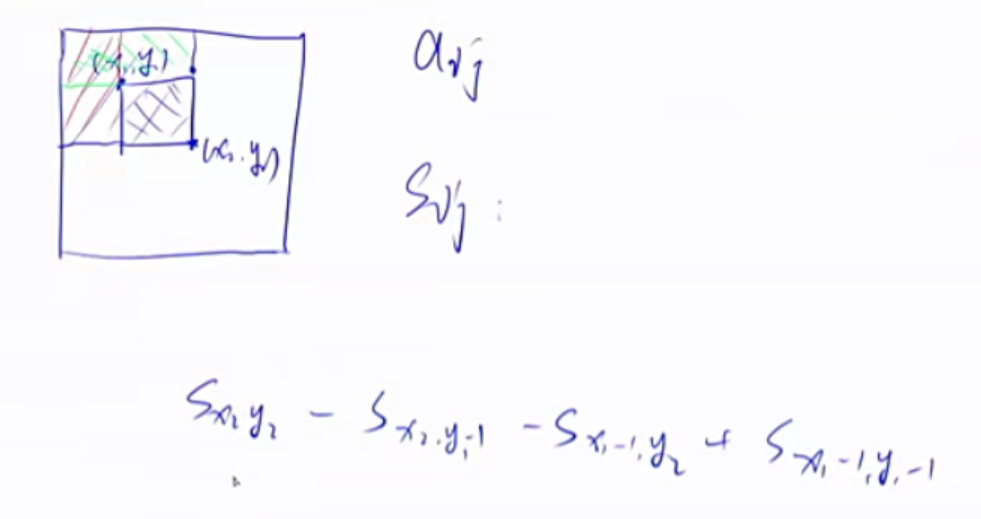
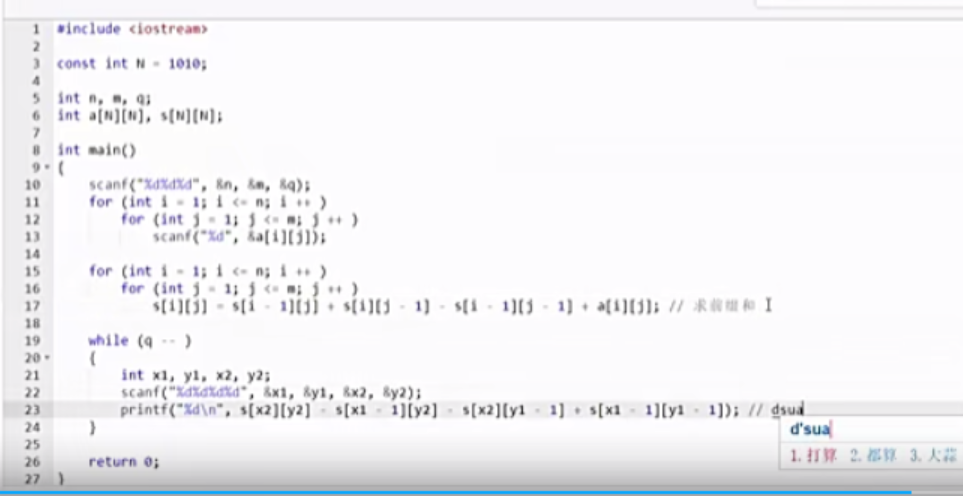
二维前缀和

二维前缀和
s[i][j]的计算方法：
二维前缀和
前缀和代码如下：
二维前缀和
边界问题：
二维前缀和

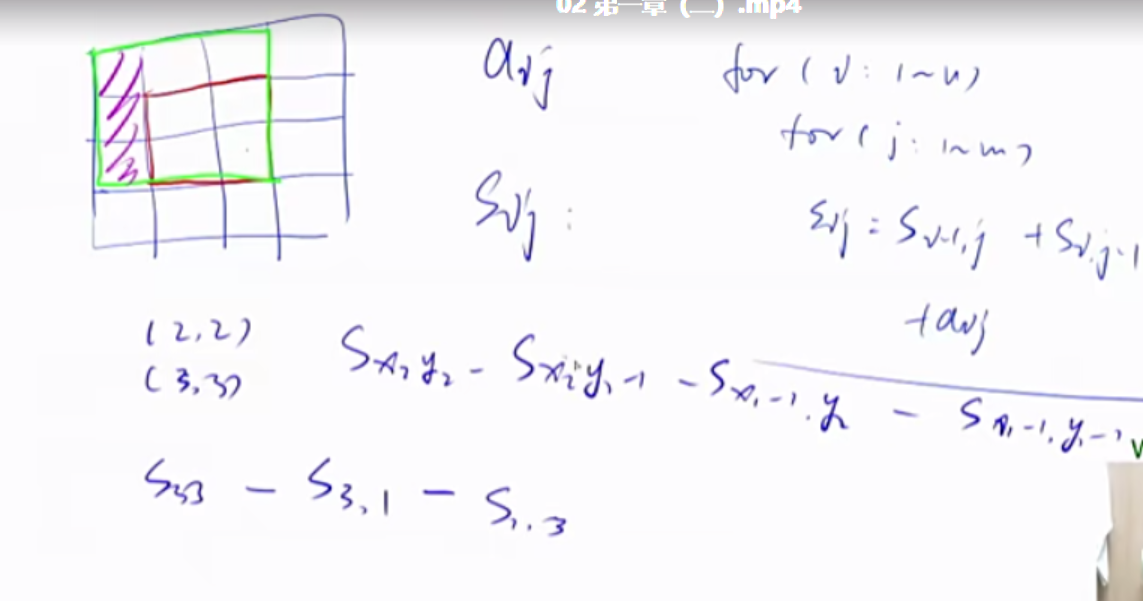
1
2
3
S[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]

练习题目
注意我们处理过程中，全部是从1开始的，从0开始的话可能会溢出。注意如果采用vector存储原始数据的话，和前缀和矩阵之间下标的关系。

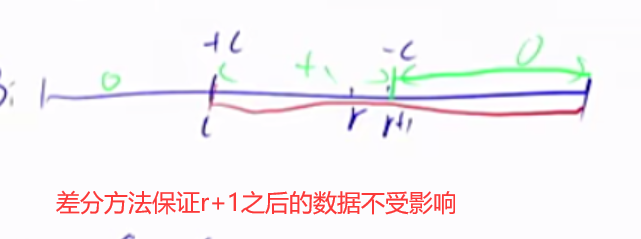
一维差分

我们有一个a数组，我们需要构造b数组，使得a数组是b数组的前缀和。
一维差分
差分的用处在于，当[l,r]区间内的所有数据全部加上一个常数C时，我们只需要$b_l+C$，那么$a_l$会自动加上C，同样$a_{l+1}$也会加上C。如果不希望$a_{r+1}$加上C，我们使$b_{r+1}-C$，这样就只有区间内的数加C了。
一维差分
在初始状态，我们假定a数组中的所有元素都是0，进而我们可以推出b数组中的所有元素也都是0，然后进行len(a)次插入操作。第一次是在(1,1)区间插入$a_1$,第二次是在(2,2)区间内插入$a_2$。

1
2
3
4
5
6
7
8
9
10
11
给区间[l, r]中的每个数加上c：B[l] += c, B[r + 1] -= c
void insert(int l,int r,int c){
    b[l]+=c;
    b[r+1]-=c;
}

//初始化差分数组b
for(int i = 1;i<=n;i++) insert(i,i,a[i]);

//还原原来的数组,方法是求前缀和，b[i] = a[1]+a[2]+...+a[i]
for(int i = 1;i<=n;i++) b[i] += b[i-1];

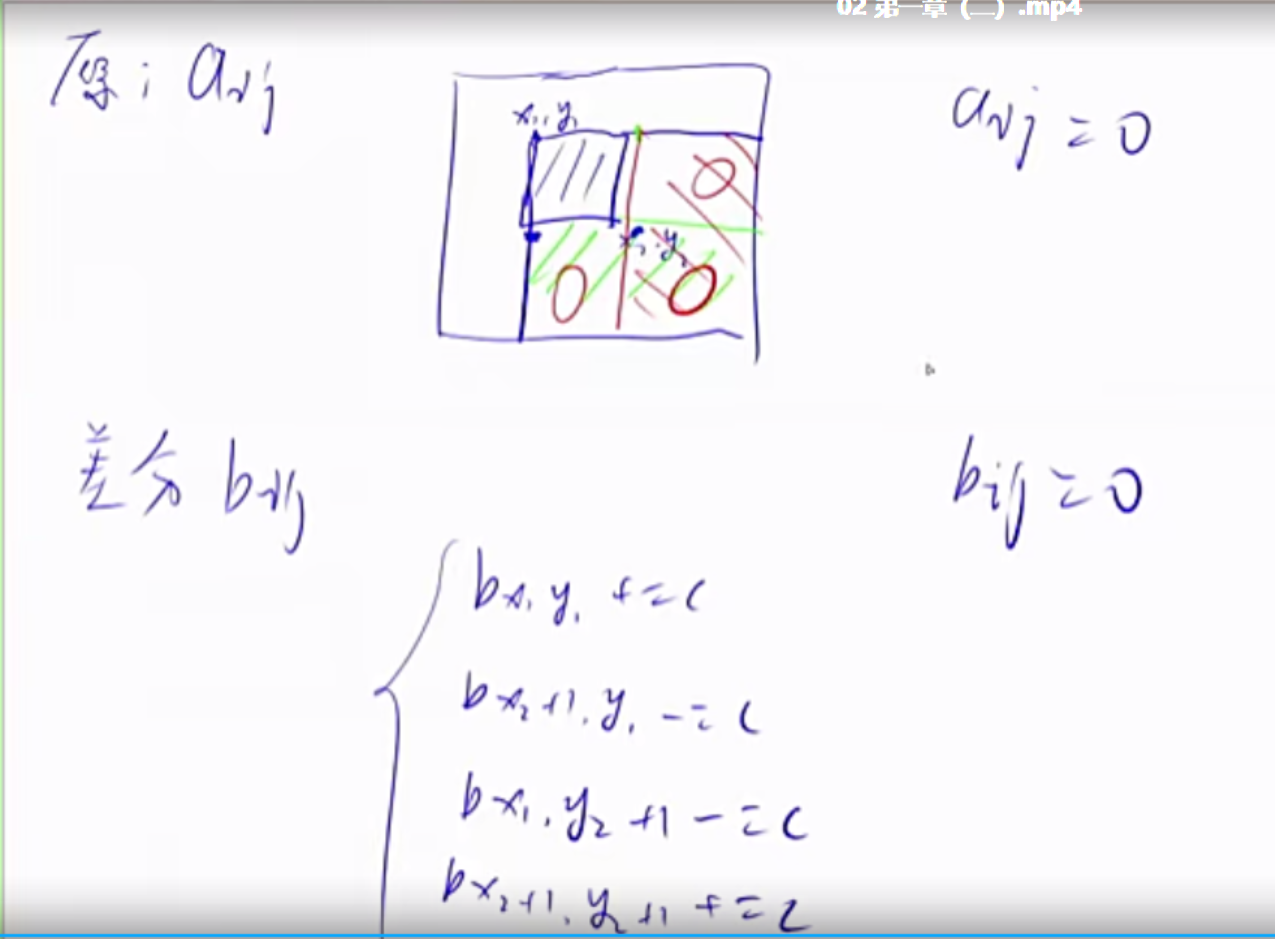
二维差分

我们有一个矩阵a，我们需要构造一个矩阵b，使得矩阵a是矩阵b的前缀和矩阵。
在初始状态，我们假定a矩阵中的所有元素都是0，进而我们可以推出来b矩阵中的所有元素也都是0，然后我们再依次将a矩阵中的值插入到b矩阵中。
给b[x][y]位置的元素加上c，效果是a矩阵中[x][y]右下角的元素全部加上c。
二维差分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c：
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c
void insert(int x1,int y1,int x2,int y2,int c){
    b[x1][y1]+=c;
    b[x2+1][y1]-=c;
    b[x1][y2+1]-=c;
    b[x2+1][y2+1]+=c;
}

//初始化差分矩阵b[n][m]
for(int i = 1;i<=n;i++){
    for(int j = 1;j<=m;j++){
        insert(i,j,i,j,a[i][j]);
    }
}

//还原原来的矩阵a，方法是求二维前缀和
for(int i = 1;i<=n;i++){
    for(int j = 1;j<=m;j++){
        b[i][j] = b[i][j-1]+b[i-1][j]+b[i][j]-b[i-1][j-1];
    }
}

还原原矩阵的依据：
二维差分
+C的快速记录法：
二维差分

位运算

位运算作为判断条件记得加括号 与&，或|，如

1
2
if((byte&0x02)==1)
//注意优先级的问题

求n的第k位数字，右移一位表示不动。
位运算

1
2
求n的第k位数字: n >> k & 1
返回n的最后一位1：lowbit(n) = n & -n

lowbit是树状数组的基本操作。在C++中是补码存储，如果n是正数，求-n的补码的规则是各位取反，末位加一，即-n = ~n+1，具体原理在第二个图中。
位运算
位运算
我们可以用lowbit(x)来求x中1的个数。基本思想是当x不是0的时候，每次减去x的最后一位1。

1
2
3
4
while(x){
    x = x-lowbit(x);
    res++;
}

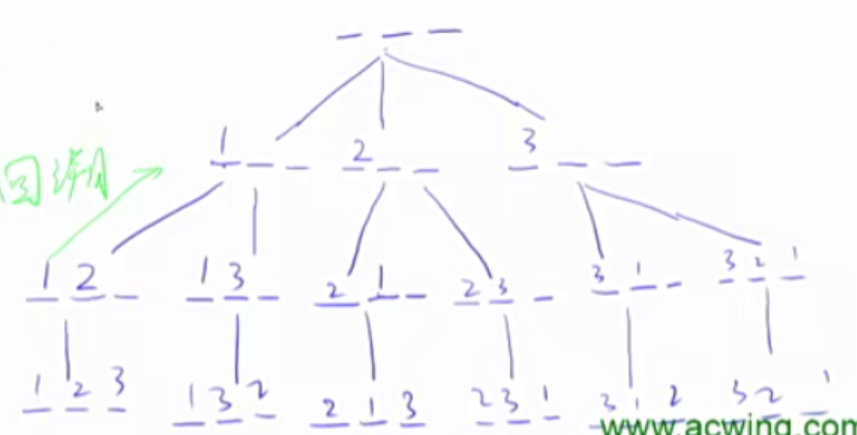
人类做题的过程实际上就是DFS的过程。

双指针算法

双指针算法的第一种形式——归并排序，一个指针指向序列A，一个指针指向序列B；第二种形式——快速排序，两个指针指向同一个序列，一个在开始的位置，一个在结束的位置。

1
2
3
4
5
6
7
8
9
10
for (int i = 0, j = 0; i < n; i ++ )
{
    //j一定要在合法的范围之内，并且满足某一种性质
    while (j < i && check(i, j)) j ++ ;

    // 具体问题的逻辑
}
常见问题分类：
    (1) 对于一个序列，用两个指针维护一段区间
    (2) 对于两个序列，维护某种次序，比如归并排序中合并两个有序序列的操作

普通算法
双指针算法最大的优势在于其时间复杂度一直都是O(n)，而上图中的普通算法复杂度为O(n^2)。一般来说我们可以先想一个朴素做法，然后再想一下如何去优化他。
例如，输入一串字符串，每个单词以空格隔开，可以用双指针实现:i指向单词的第一个位置，j指向单词后的空格。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include<iostream>
#include<string>
using namespace std;
int main(){
    char str[1000];
    gets(str);
    int n = strlen(str);
    for(int i = 0;str[i];i++){
        int j = i;
        while(j<n&&str[j]!=' ') j++;
        //这道题的具体处理逻辑
        for(int k = i;k<j;k++){
            cout<<str[k];
        }
        cout<<endl;
        //这样在循环开头i++正好指向下一个单词的开头
        i = j;
    }
}

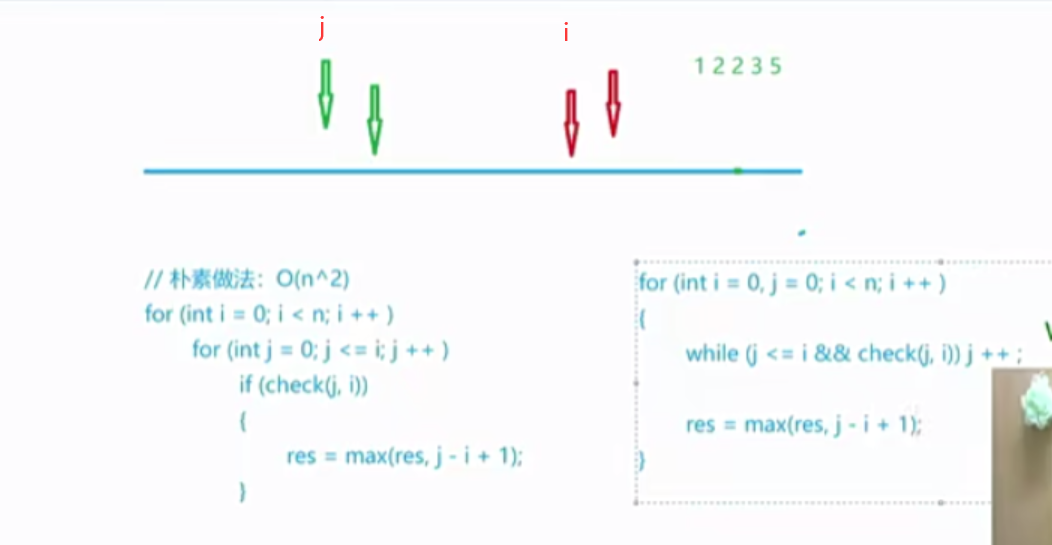
双指针算法寻找序列中的连续最长不重复子序列。
普通算法
左边max应该是i-j+1。
图中的check方法是确定(j,i)之间是否有重复元素。具体方法是开一个大小等于数据范围的数组。具体方法图下图：
普通算法
当我们发现(j,i)区间内有重复的时候，那么重复的一定是刚刚加入的a[j],因此我们check处的条件可以替换为$a_j!=a_i$,将j指针一直移动到和$a_i$重复的元素的位置。
该题目的关键代码为：

1
2
3
4
5
6
7
8
9
//a是数据,s是次数数组，n是数据的个数
for(int i = 0,j = 0;i<n;i++){
    s[a[i]]++;
    while(s[a[i]]>1){
        s[a[j]]--;
        j++;
    }
    res = max(res,i-j+1);
}

离散化

整数的离散化，保序的离散化。输入的数据范围非常大，但是个数比较少。当我们在处理过程中要以输入的数据作为下标时，我们可以采用离散化的方法把他们映射到从0开始的自然数。
离散化
离散化第一步中去重的工作，是由unique函数和erase方法搭配完成的。
离散化
离散化的本质是坐标映射。
离散化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
vector<int> alls; // 存储所有待离散化的值
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end());   // 去掉重复元素
//unique方法的作用在于将数组去重，并返回数组的尾端点

// 二分求出x对应的离散化的值
int find(int x) // 找到第一个大于等于x的位置
{
    int l = 0, r = alls.size() - 1;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1; // 映射到1, 2, ...n，如果不加1，从0开始
}

例子：区间和的查询，在数据范围小的情况下可以用前缀和来解决，在数据范围大的情况下，就需要用离散化进行一个坐标的映射，再使用前缀和处理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include<iostream>
#include<vector>
#include<algorithm>

using namespace std;

using PII = pair<int,int>;

const int N = 300010;

int n,m;
int a[N],s[N];

vector<int> alls;
vector<PII> add,query;

//find函数的目标是≥x的最小的数,mid有可能是答案
int find(int x){
    int l = 0,r = alls.size()-1;
    while(l<r){
        mid = (l+r)>>1;
        if(alls[mid]>=x){
            r = mid;
        }else{
            l = mid+1;
        }
    }
    return r+1;//映射到从1开始的自然数
}

int main(){
    cin>>n>>m;
    for(int i = 0;i<n;i++){
        int x,c;
        cin>>x>>c;
        add.push_back({x,c});
        alls.push_back(x)
    }
    for(int i = 0;i<m;i++)
    {
        int l,r;
        cin>>l>>r;
        query.push_back({l,r});
        alls.push_back(l);
        alls.push_back(r);
    }
    //我们已经把所有要用到的下标全部放入到alls数组中，接下来是把alls数组中的元素去重
    sort(alls.begin(),alls.end());
    //erase方法是把begin到end的元素全部删掉
    alls.erase(unique(alls.begin(),alls.end()),alls.end());

    //插入操作
    for(auto item:add){
        int x = find(item.first);
        a[x]+=item.second;
    }

    //前缀和预处理 alls.size()就是我们用到的最大的坐标
    for(int i = 1;i<=alls.size();i++){
        s[i] = s[i-1]+a[i];
    }

    //处理询问
    for(auto item:query){
        int l = find(item.first),r = find(item.second);
        cout<<s[r]-s[l-1]<<endl;
    }
}

unique函数的原理，双指针原理：如果i是第一个元素(i == 0)或者a[i]!=a[i-1],那么他就不是重复元素。就令a[j++] = a[i]
双指针算法，一个指针i用来遍历数组，另一个指针j用来记录当前存储的元素位置。
最终从0到j-1就都是不重复的元素，我们返回a.begin()+j就可以。
练习题目

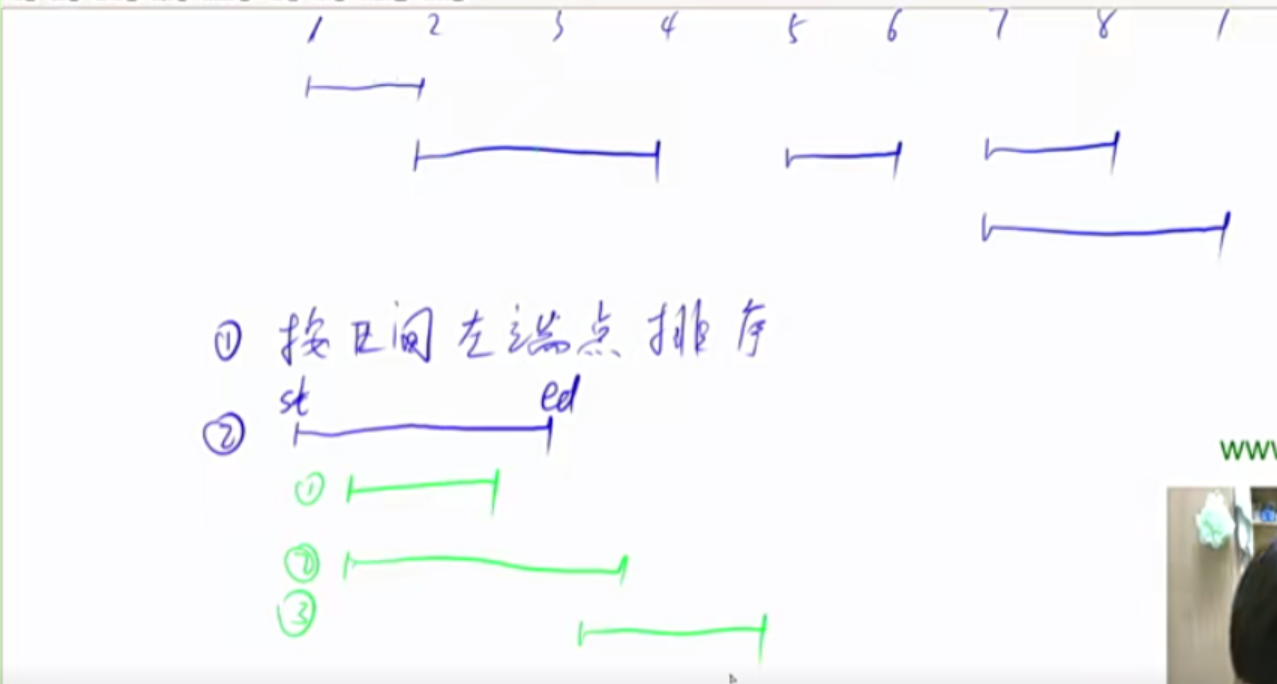
区间合并

区间合并的功能在于快速地将两个有交集的区间进行合并。
规定：两个区间即使只有端点相交也会进行合并。
区间合并
下一个区间的三种情况：
1）包含->当前维护区间不变
2）有交集但是有一部分出去了->当前维护区间右端点变大
3）没有交集->当前维护区间左右端点都变化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
// 将所有存在交集的区间合并
void merge(vector<PII> &segs)
{
    vector<PII> res;

    //在处理之前先对区间排序，pair排序有限对左端点排序
    sort(segs.begin(), segs.end());

    //在排序之前我们预设边界值，实际上就是-∞到＋∞
    int st = -2e9, ed = -2e9;
    for (auto seg : segs)
        if (ed < seg.first)//发现了一个新的区间
        {
            //如果这个区间不是我们初始的区间，我们就将它加到答案里去
            if (st != -2e9||segs[0].first == -2e9) res.push_back({st, ed});
            //更新当前区间两个端点
            st = seg.first, ed = seg.second;
        }
        //否则当前区间和seg区间有交集，我们只需要更新区间右端点
        else ed = max(ed, seg.second);

    //我们需要单独将循环结束时的当前区间加入到答案中去，加一个判断的目的是为了防止输入中没有输入任何区间
    if (st != -2e9) res.push_back({st, ed});

    segs = res;
}

int main(){
    cin>>n;

    for(int i = 0;i<n;i++){
        int l,r;
        cin>>l>>r;
        segs.push_back({l,r});
    }

    merge(segs);
}

练习题目

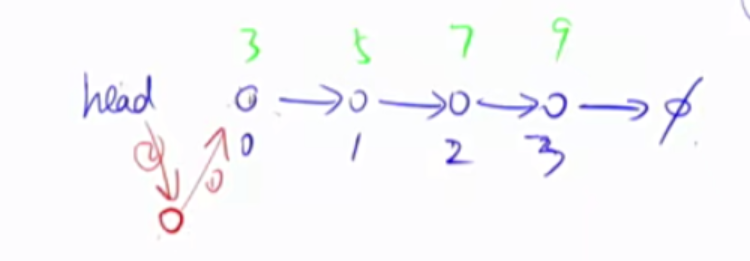
单链表

数组模拟实现(静态链表)。用的最多的是邻接表。邻接表的本质是n个链表。它的基本应用是存储图和树。
单链表
单链表
空节点的下标用-1来表示。
在实现中我们使用头插法来插入新节点。头节点由原来的A指向新插入的节点，新插入的节点的next指针指向A。
单链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
// head存储链表头，e[]存储节点的值，ne[]存储节点的next指针，idx表示当前用到了哪个节点，就是当前处理的节点
int head, e[N], ne[N], idx;

// 初始化,在实现过程中一定不能忘记初始化
void init()
{
    head = -1;
    idx = 0;
    //每个点都没有被分配，当前可以从0节点开始使用
}

// 在链表头插入一个数a
void insert(int a)
{
    e[idx] = a, ne[idx] = head, head = idx ++ ;
}

// 将头结点删除，需要保证头结点存在，在链表删除节点中，如果删除的是头节点，那么需要对头指针进行处理，否则就是正常的删除remove。
void remove()
{
    head = ne[head];
}

//将一个数a插入到编号为k的节点后面
//step1 a->next = k->next
//step2 k->next = a
void add(int k,int a){
    e[idx] = a;
    ne[idx] = ne[k];
    ne[k] = idx;
}

//将下标为k的节点的下一个节点m删除
//直接将k->next = m->next
//一般来说，删掉了一个点之后我们不管idx，就当这个点不存在
void remove(int k){
    ne[k] = ne[ne[k]];
}

//遍历链表写法
for(int i = head;i!=-1;i = ne[i]){
    cout<<e[i]<<" ";
}

注意在该模板中，下标为0的是第一个插入的节点。
单链表无法找到a节点的上一个节点。

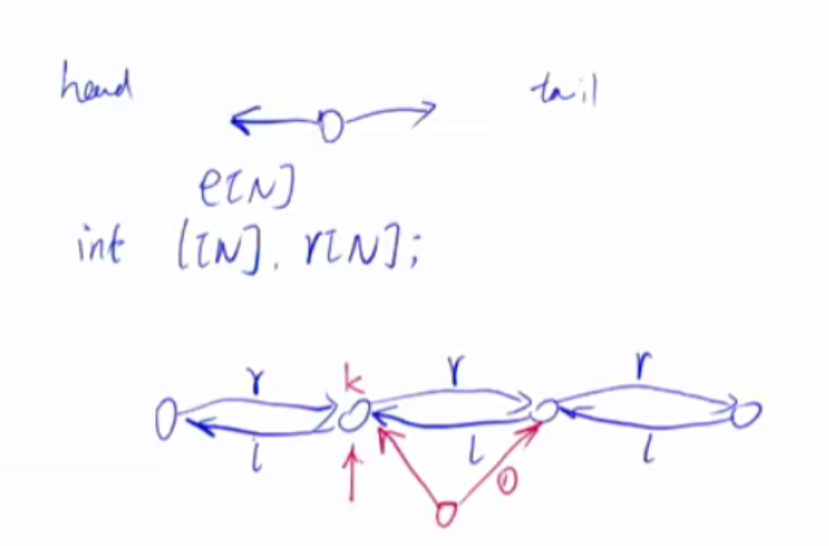
双链表

双链表的作用是优化某些问题。
双链表
双链表的插入操作。
双链表
双链表的删除操作。
双链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// e[]表示节点的值，l[]表示节点的左指针，r[]表示节点的右指针，idx表示当前用到了哪个节点
int e[N], l[N], r[N], idx;

// 初始化
void init()
{
    //0是左端点，1是右端点
    //此时链表的状态是0-1，因此0号节点的右边是1号节点，1号节点的左边是0号节点
    r[0] = 1, l[1] = 0;
    idx = 2;
}

// 在节点a的右边插入一个数x
//如果需要在节点a的左边插入一个数x，调用insert(l[a])
void insert(int a, int x)
{
    e[idx] = x;
    l[idx] = a, r[idx] = r[a];
    //注意下面这两个语句不能写反了
    l[r[a]] = idx, r[a] = idx ++ ;
}

// 删除节点a
void remove(int a)
{
    l[r[a]] = l[a];
    r[l[a]] = r[a];
}

模拟栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// tt表示栈顶，初始值为0
int stk[N], tt = 0;

// 向栈顶插入一个数
stk[ ++ tt] = x;

// 从栈顶弹出一个数
tt -- ;

// 栈顶的值
stk[tt];

// 判断栈是否为空
if (tt > 0)
{
    //此时栈不是空的
}

队列

普通队列

在队尾插入元素，在队头弹出元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// hh 表示队头，tt表示队尾，注意tt的初值为-1.
int q[N], hh = 0, tt = -1;

// 向队尾插入一个数
q[ ++ tt] = x;

// 从队头弹出一个数
hh ++ ;

// 队头的值
q[hh];

// 判断队列是否为空
if (hh <= tt)
{
    //此时队列不为空
}

循环队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// hh 表示队头，tt表示队尾的后一个位置
int q[N], hh = 0, tt = 0;

// 向队尾插入一个数
q[tt ++ ] = x;
if (tt == N) tt = 0;

// 从队头弹出一个数
hh ++ ;
if (hh == N) hh = 0;

// 队头的值
q[hh];

// 判断队列是否为空
if (hh != tt)
{

}

单调栈

单调栈的典型应用：1）链表与邻接表 2）栈与队列 3）KMP
单调栈1
下图为暴力解法
单调栈2
找到$a_i >a_j$的位置输出$a_j$。
暴力做法的实质是有一个栈，在i指针右移的过程中，不断将i指针左边的元素入栈。然后从栈顶开始找符合要求的元素。但是这种方法我们可以发现，有些元素怎样都不会成为答案。例如在数组中，若$a_3>a_5$，那么$a_3$永远不会成为答案。因为如果$a_i>a_3$，那么$a_i>a_5$一定成立，但是$a_5$一定距离i点更近。
单调栈3
单调栈内的数据特点如图，不符合的点全部删掉。每次一个新的点入栈的时候，如果栈顶$top>a_{in}$，那么栈顶就可以删掉，因为它变成了永远不会成为答案的元素。当$ top< a_i $ 时，top就是我们要找的点。
练习题目

1
2
3
4
5
6
7
常见模型：找出每个数左边离它最近的比它大/小的数
int tt = 0;
for (int i = 1; i <= n; i ++ )
{
    while (tt && check(stk[tt], i)) tt -- ;
    stk[ ++ tt] = i;
}

例题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<iostream>

using namespace std;

const int N = 100010;

//n是输入的数据个数
int n;
//tt表示栈顶的位置
int stk[N],tt;

int main(){
    cin>>n;
    //如果是左边就是正序，如果要求的是右边就是逆序，关键点是想清楚什么情况下这个元素没用
    for(int i = 0;i<n;i++){
        int x;
        cin>>x;
        //当当前栈不空的时候，且待插入的x≤栈顶top时，将top出栈
        //单调栈的精髓就在于不断排除掉不是答案的元素
        //注意啊，这里要清楚单调栈里面存的是元素还是索引
        while(tt&&stk[tt]>=x){
            tt--;
        }
        //此时如果栈不空，则栈顶元素即为x左边距离最近且小于x的元素
        if(tt) cout<<stk[tt]<<endl;
        //否则栈是空的，说明x的左边没有任何一个元素比它小，返回-1
        else cout<<-1<<endl;
        //最后把x入栈，任何情况都入栈
        stk[++tt] = x;
    }
}

//读优化
cin.tie(0);
ios::sync_with_stdio(false);

单调队列

保证队列里存的都是当前窗口的所有元素，在队列满了之后，每滑动一次窗口，就要先把滑出窗口的元素出队，再将滑入窗口的元素入队。
练习题目
例题是练习题目的改版，是要求区间中的最小值。
单调队列1
单调队列的精髓也在于及时去掉不可能成为答案的元素，比如上图中的3，只要-3在队列中，3就永远不可能成为答案，而-3还是不可能比3早出队列的，因此我们可以把3删掉。-1也是同理，可以删掉。
我们可以归纳出删掉元素a的特征：a在b的前面，且a>b，那么我们删掉a。
单调队列2
上图就是删掉不可能成为答案的元素之后，单调队列中元素的特征。如果我们要求一个严格单调上升队列的最小值，就是该队列的第一个元素。在有单调性的队列中，也可以用二分查找。多重背包有可以用单调队列优化。
单调队列中存的不是值，是下标。
用数组模拟的队列的好处，是比stl速度更快。

1
2
3
4
5
6
7
8
常见模型：找出滑动窗口中的最大值/最小值
int hh = 0, tt = -1;
for (int i = 0; i < n; i ++ )
{
    while (hh <= tt && check_out(q[hh])) hh ++ ;  // 判断队头是否滑出窗口
    while (hh <= tt && check(q[tt], i)) tt -- ;
    q[ ++ tt] = i;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include<iostream>

using namespace std;

const int N = 1000010;

int n,k;
int a[N],q[N];

int main(){
    scanf("%d %d",&n,&k);
    for(int i = 0;i<n;i++){
        scanf("%d",&a[i]);
    }
    //定义队列头和队列尾
    int hh = 0,tt = -1;
    for(int i = 0;i<n;i++){
        //使用if而不是while的原因是每一次窗口只会向后移动一位，我们只要进行一次出队操作
        //判断队头是否已经滑出了窗口
        //第一个条件是判断队列是否为空
        //第二个条件，当前的终点是i，起点应该是i-k+1，当队首元素的索引在起点之前时，就应该出队了
        if(hh<=tt&(i-k+1>q[hh])){
            hh++;
        }
        //如果新入队的数比原来队尾的数要小的话，原来队尾就不可能成为答案，我们将队尾出队
        while(hh<=tt&&a[q[tt]]>=a[i]){
            tt--;
        }
        //把当前的这个数插入队列
        //这个要插入的值可能会把队列中的元素全部挤出去，因此要先入队，然后再输出答案。
        q[++tt] = i;
        //从第k个数开始才有输出，在此之前没有输出
        if(i>=k-1){
            printf("%d ",a[q[hh]]);
        }

        //上面是最小值，下面是最大值
        if(hh<=tt&&(i-k+1>q[hh])){
            hh++;
        }
        //如果新入队的数比原来队尾的数要大的话，原来队尾就不可能成为答案，我们将队尾出队
        while(hh<=tt&&a[q[tt]]<=a[i]){
            tt--;
        }
        //把当前的这个数插入队列
        q[++tt] = i;
        //从第k个数开始才有输出，在此之前没有输出
        if(i>=k-1){
            printf("%d ",a[q[hh]]);
        }
    }
    return 0;
}

KMP

01:57:23
KMP下标习惯从1开始
KMP1
上图中是朴素的字符串匹配算法。
KMP2
上图说明了’next[i] = j’的含义是p数组中从1到j的元素和p数组中从i-j+1到i的元素全部相等。
KMP3
上图中显示的是P串和S串的坐标对应关系，当模式串P在j+1处和S串不相等时，我们直接调用next[j],将j赋值为next[j]，则此时P串完成了后移。

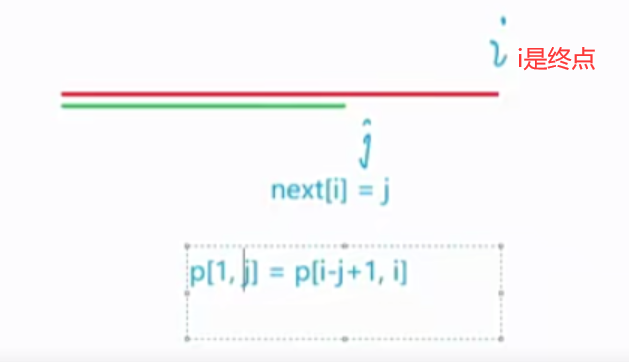
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// s[]是长文本，p[]是模式串，n是s的长度，m是p的长度
求模式串的Next数组：
for (int i = 2, j = 0; i <= m; i ++ )
{
    while (j && p[i] != p[j + 1]) j = ne[j];
    if (p[i] == p[j + 1]) j ++ ;
    ne[i] = j;
}

// 匹配
for (int i = 1, j = 0; i <= n; i ++ )
{
    while (j && s[i] != p[j + 1]) j = ne[j];
    if (s[i] == p[j + 1]) j ++ ;
    if (j == m)
    {
        j = ne[j];
        // 匹配成功后的逻辑
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include<iostream>

using namespace std;

const int M = 10010,M = 100010;

int n,m;
char p[N],s[M];
int ne[N];

int main(){
    cin>>n>>p+1>>m>>s+1;
    //求next数组的过程
    //如果第一个位置失败了，那么就只能回退到第0个位置。所以循环初值j = 0
    next[1] = 0
    for(int i = 2,j = 0;i<=n;i++){
        while(j&&p[i]!=p[j+1]){
            j = ne[j];
        }
        if(p[i] == p[j+1]){
            j++;
        }
        ne[i] = j;
    }

    //kmp匹配过程
    //从上图可以看出来，试图和s[i]匹配的是p[j+1],这两个之间错了一位
    for(int i = 1,j = 0;i<=m;i++){
        //如果j没有退回起点且当前值不匹配的话,直到j已经退到开头，退无可退，或是当前值匹配上了
        while(j&&s[i]!=p[j+1]){
            j = ne[j];
            //如果是当前值匹配上了，j就可以下移
            if(s[i]==p[j+1]){
                j++;
            }
            //如果j == n，说明匹配成功
            if(j == n){
                //success!输出匹配的起始位置
                printf("%d ",i-n+1);
                //匹配成功之后向后退一步
                j = ne[j];            
            }
        }
    }
    return 0;
}

使用定义计算next数组时，前缀是从左到右，后缀也是从左到右看。第i个公共前缀的长度必须小于i。
练习题目
05

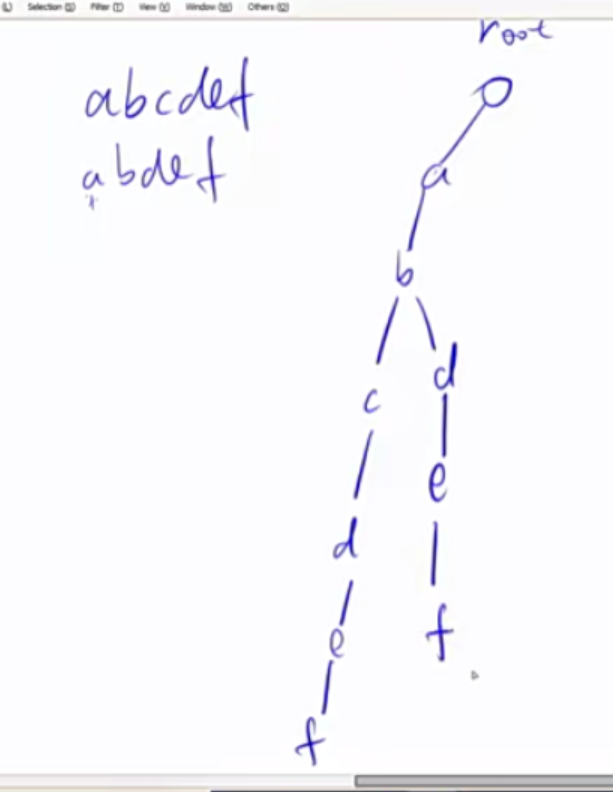
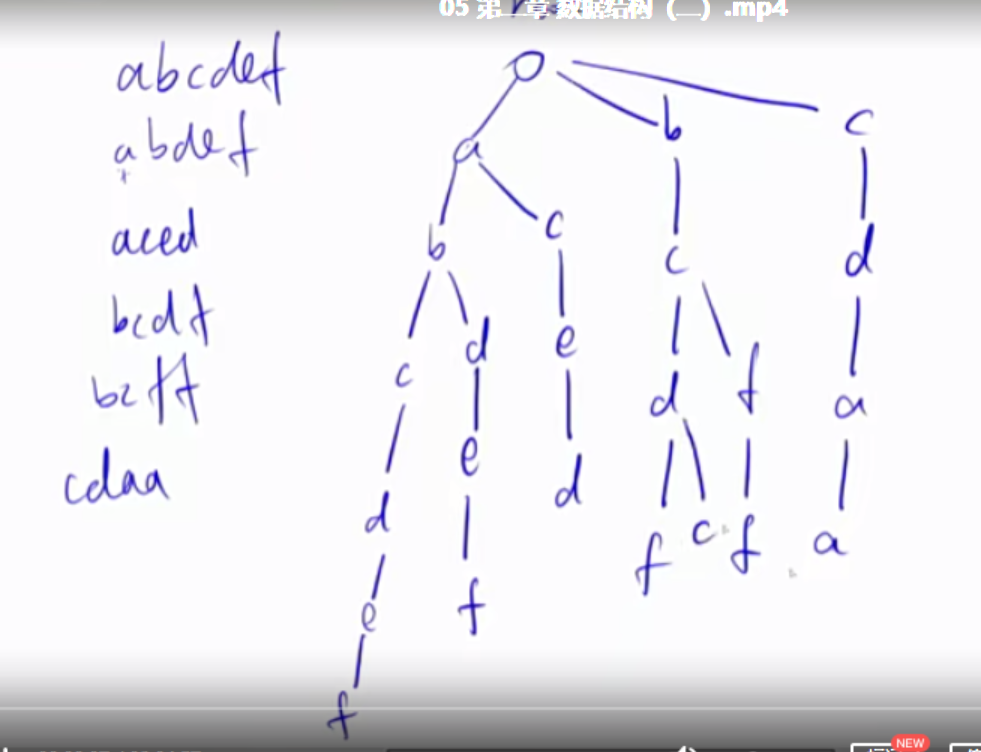
Trie树

Trie树是用来高效地存储和查找字符串集合。使用trie的题目中字符串一般要么全是小写字母，要么全是大写字母，要么全是数字。下图是一个例子，我们用该字符串集合创建一个Trie树。
Trie树1
在将第一个字符串插入到Trie树后，此时的树为
Trie树2
在插入第二个字符串之后Trie树的状态为
Trie树3
依次类推，最终的Trie树为
Trie树4
我们会在每个字符串结尾处打一个标记。否则如果有一个单词是另一个单词的前缀，我们在树中很有可能发现不了这个单词。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
int son[N][26], cnt[N], idx;
// 0号点既是根节点，又是空节点
// son[][]存储树中每个节点的子节点
// cnt[]存储以每个节点结尾的单词数量

// 插入一个字符串
void insert(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if (!son[p][u]) son[p][u] = ++ idx;
        p = son[p][u];
    }
    cnt[p] ++ ;
}

// 查询字符串出现的次数
int query(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if (!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
}

例题，统计字符串出现的次数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include<iostream>

using namespace std;

const in N = 100010;

//因为只有26个字母，因此每个子节点最多会引出26条边
//cnt存的是以当前这个点结尾的单词的个数
//idx和单链表中的idx是一个意思，表示当前用到了哪个节点，就是当前处理的节点
//下表是0的点，既是根节点，又是空节点。
int son[N][26],cnt[N],idx;

//插入
void insert(char str[]){
    //初始化节点编号
    int p = 0;
    //在c++中字符串的结尾是\0,因此可以用str[i]来判断是否走到结尾
    for(int i = 0;str[i];i++){
        //需要把小写字母a-z映射成0-25
        int u = str[i]-'a';
        //如果p这个节点不存在u这个儿子的话，我们就把他创建出来
        if(!son[p][u]){
            son[p][u] = ++idx;
        }
        //将p指向当前节点
        p = son[p][u];
    }
    //结束的时候p对应的点就是一个字符串中最后一个字母所在的点
    cnt[p]++;
}

//查询，返回字符串出现的次数
//查询操作和插入操作类似
int query(char str[]){
    //从根节点出发
    int p = 0;
    for(int i = 0;str[i];i++){
        int u = str[i]-'a';
        //如果它不存在该子节点的话，证明集合中不存在这个单词，返回0
        if(!son[p][u]){
            return 0;
        }
        //否则就走过去
        p = son[p][u];
    }
    return cnt[p];
}

练习题目
练习题目
00:25:40

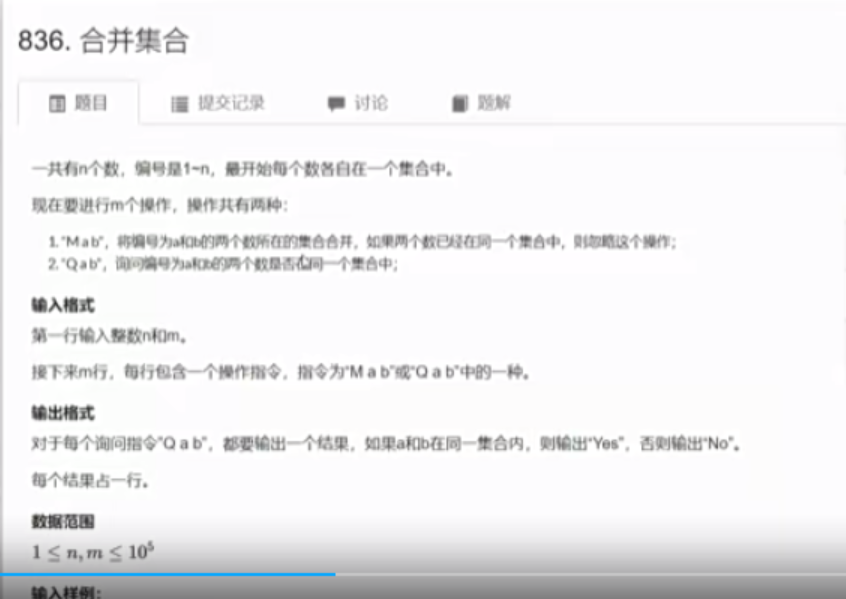
并查集

并查集的特点：1）将两个集合合并；2）询问两个元素是否在一个集合当中。
并查集可以在近乎O(1)的时间复杂度内完成这两个操作。
并查集1
并查集的结构如上图，father节点，最后一个集合有一个代表元素。
并查集的基本原理：每一个集合用一棵树来表示。树根的编号就是整个集合的编号。每个节点存储存储他的父节点，p[x]表示x的父节点。
问题1：如何判断树根 if(p[x] == x),这也意味着，除了根节点之外，p[x]!=x。
问题2：如何求x的集合编号 while(p[x]!=x)x = p[x];
问题3：如何合并两个集合 p[x]是x的集合编号，p[y]是y的集合编号，p[x] = y就是合并了两个集合。
一般按秩合并优化不怎么明显，如果要优化，推荐路径压缩。

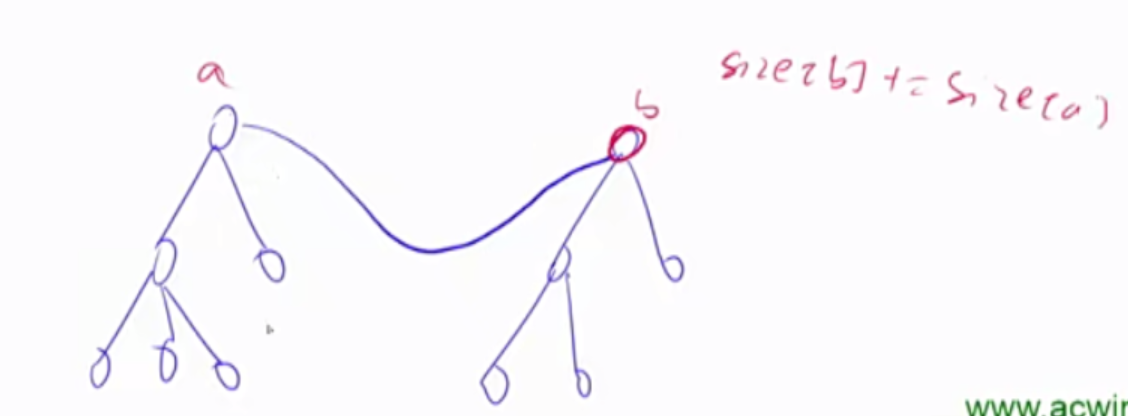
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
(1)朴素并查集：

    int p[N]; //存储每个点的祖宗节点

    // 返回x的祖宗节点，如果并查集中x的范围过于大，p数组开不了这么大，可以考虑使用离散化
    int find(int x)
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ ) p[i] = i;

    // 合并a和b所在的两个集合：
    p[find(a)] = find(b);


(2)维护size的并查集：

    int p[N], size[N];
    //p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义，表示祖宗节点所在集合中的点的数量

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        size[i] = 1;
    }

    // 合并a和b所在的两个集合：
    size[find(b)] += size[find(a)];
    p[find(a)] = find(b);


(3)维护到祖宗节点距离的并查集：

    int p[N], d[N];
    //p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x)
        {
            int u = find(p[x]);
            d[x] += d[p[x]];
            p[x] = u;
        }
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        d[i] = 0;
    }

    // 合并a和b所在的两个集合：
    p[find(a)] = find(b);
    d[find(a)] = distance; // 根据具体问题，初始化find(a)的偏移量

例题题目如下：
并查集2
例题加强版：
并查集3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include<iostream>

using namespace std;

const int N = 10010;

int n,m;
int p[N];
//记录每个集合的大小,规定只保证根节点的size是有意义的
int size[N];

int find(int x){//返回x的祖宗节点，带路径压缩
    if(p[x]!=x){
        //如果x不是根节点，就让p[x]等于它的祖宗节点
        //本质上就是进一步查找父节点的操作
        p[x] =find(p[x]);
        //当这个递归在回溯的时候，会将路径上每一个节点都指向父节点
    }
    return p[x];
}

int main(){
    //读入操作数
    cin>>n>>m;
    scanf("%d %d",&n,&m);
    //初始化p数组
    for(int i = 1;i<=n;i++){
        p[i] = i;
        size[i] = 1;
    }
    while(m--){
        //scanf()有一些缺点，如果读入的是一个简单的字符，那么就会读入空格、回车等一些内容，但是如果读入的是字符串，就会自动忽略空格和回车
        char op[2];
        int a,b;
        scanf("%s %d %d",op,&a,&b);

        if(op[0] == 'M'){
            //让a祖宗节点的父亲等于b的祖宗节点
            //特判当a和b已经在一个集合中
            if(find(a)==find(b)){
                continue;
            }
            p[find(a)] = find(b);
            size[find(b)]+=size[find(a)];
        }else if(op[0]=='Q'){
            if(find(a) == find(b)){
                printf("yes");
            }else{
                printf("no");
            }
        }else{
            scanf("%d",&a);
            printf("%d\n",size[find(a)]);
        }
    }
    return 0;
}

在一个连通块中，a可以到达b，b也可以到达a。
下图为更新size的思路，b为更新后的根节点。
并查集4
01：09：49

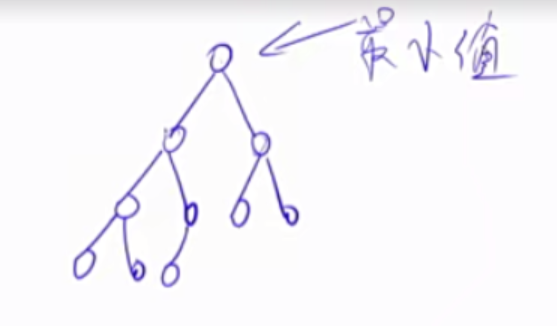
堆

堆的基本操作：1）插入一个数 2）求集合当中的最小值 3）删除最小值 (前三个STL支持) 4）删除任意一个元素 5）修改任意一个元素。
堆的特点：是一个完全二叉树，除了最后一层节点不满，从左到右排列。
小根堆：每一个点都是小于等于左右儿子的。
堆1
堆的存储如下：
堆2
两个基本操作，down和up。
下标是从1开始的，因为如果从0开始的，2x结果就还是0，冲突了。

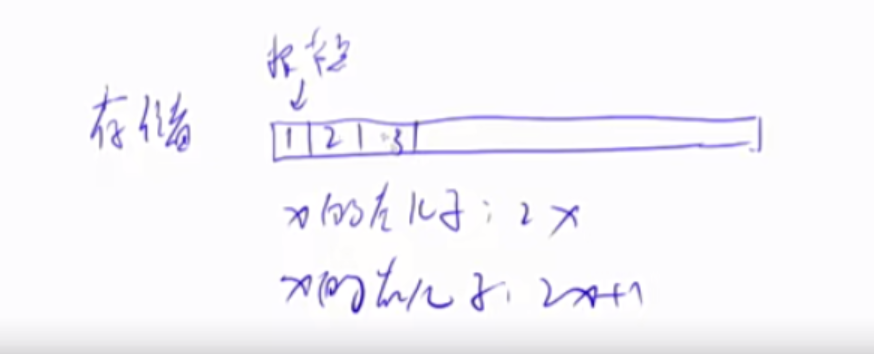
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
// h[N]存储堆中的值, h[1]是堆顶，x的左儿子是2x, 右儿子是2x + 1
// ph[k]存储第k个插入的点在堆中的位置 p是数组下标pointer，h是堆heap的意思
// hp[k]存储堆中下标是k的点是第几个插入的,在交换时用于寻找ph数组中对应的位置 ph[k] = j hp[j] = k
int h[N], ph[N], hp[N], size;

// 交换两个点，及其映射关系
void heap_swap(int a, int b)
{
    swap(ph[hp[a]],ph[hp[b]]);
    swap(hp[a], hp[b]);
    //主要用到这一句
    swap(h[a], h[b]);
}

//如果把一个值变大了，就要往树的下面移
void down(int u)
{
    //t表示最小值
    int t = u;
    //判断有没有左儿子，如果左儿子存在并且左儿子的值小于h[t]，那么t就是左儿子
    if (u * 2 <= size && h[u * 2] < h[t]) t = u * 2;
    //同理判断右儿子
    if (u * 2 + 1 <= size && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    //如果u不等于t，也就意味着当前根节点不是存的最小值，我们需要对堆进行维护
    if (u != t)
    {
        heap_swap(u, t);
        down(t);
    }
}

void up(int u)
{
    //只要我有父节点并且我父节点比u节点要大的话
    while (u / 2 && h[u] < h[u / 2])
    {
        //交换u节点和父节点
        heap_swap(u, u / 2);
        //u/2
        u >>= 1;
    }
}

// O(n)建堆，如果是用插入的操作的话会需要nlogn的复杂度
//注意一定要从下往上递归，不可以逆着来
for (int i = n / 2; i; i -- ) down(i);

//操作一
void insert(int x){
    //在堆的最后插入一个值,然后把这个数不断往上移
    h[++size] = x;
    up(size);
}

//操作二
//求堆中的最小值
return h[1];

//操作三
//先用最后一个点覆盖掉根节点，然后把最后一个点删掉，然后维护堆
h[1] = h[size];
size--;
down(1);
//如果要删掉第k个点，操作四
h[k] = h[size];
size--;
//变大就往下走
down(k);
//变小就往上走,这两个操作只有一个
up(k); 

//操作五
h[k] = x;
down(k);
up(k);

06

哈希表

哈希表1
哈希函数的映射方法一般是简单地取模，但是要求是一个质数，而且这个质数要距离2的整次幂尽可能的远。
离散化是一种特殊的哈希方式，因为离散化的hash结果要求保序。
拉链法，创建一个大小为模的大小的数组，看成链表头节点的集合，然后用数据hash后值作为索引，寻找对应的头节点，将该数据插入到该头节点对应的链表中。有点类似于桶排序。
hash算法是一个期望算法，每条链上的元素可以认为是常数个。
要实现删除，一般是创建一个数据，为删除的元素打上一个标记。
哈希表的时间复杂度是O(1)，一般是不会和sort结合使用。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
(1) 拉链法
    //h是链表头节点的集合，剩下的数据和变量用于实现链表
    int h[N], e[N], ne[N], idx;
    //把链表头先清空
    //空指针一般用-1来表示
    //在cstring库中
    memset(h,-1,sizeof(h));

    // 向哈希表中插入一个数
    void insert(int x)
    {
        //在C++中，如果x是负数，则取模结果也是负数，为了保证结果是正数，需要再加上一个N
        int k = (x % N + N) % N;
        e[idx] = x;
        //h[k]记录了插入前位于链表首部的元素索引
        ne[idx] = h[k];
        //让头节点指向当前插入的节点
        h[k] = idx ++ ;
    }

    // 在哈希表中查询某个数是否存在
    bool find(int x)
    {
        int k = (x % N + N) % N;
        //从头开始遍历k对应的链表
        for (int i = h[k]; i != -1; i = ne[i])
            if (e[i] == x)
                return true;

        return false;
    }

(2) 开放寻址法
    //实现删除，就是调用查找函数，在删除数组中打一个标记
    //N的大小为题目范围的2~3倍大
    int h[N];
    int null = 0x3f3f3f3f;
    //我们在输入数据范围之外选择一个数作为空的标志
    //meset是按照字节进行初始化的
    memset(h,0x3f,sizeof(h));
    //memset(h,-1,sizeof(h))把每一个位都初始化位1，最后int的结果为-1

    // 如果x在哈希表中，返回x的下标；如果x不在哈希表中，返回x应该插入的位置
    int find(int x)
    {
        int t = (x % N + N) % N;
        //如果当前的位置上有数据且不和x相等的话，就向后移动
        while (h[t] != null && h[t] != x)
        {
            t ++ ;
            //如果已经看完最后一个位置，就需要循环看第一个位置
            if (t == N) t = 0;
        }
        return t;
    }

    void insert(int x){
        int k = find(x);
        h[k] = x;
    }

    void find_elem(int x){
        int k = find(x);
        if(h[k]!=null){
            cout<<"Yes"<<endl;
        }else{
            cout<<"No"<<endl;
        }
    }

00：47：20
字符串前缀哈希法。首先预处理好所有前缀的哈希。定义h[0] = 0。
哈希表2
根本思路是把字符串看成p进制的数字。例子如下:
哈希表3
通过模Q可以将该字符串映射到0~Q-1的范围上去。
注意：不能将字母映射到0。比如A映射成0，那么字符串AA映射成00，这就导致不同的字符串有了相同哈希值。
而且假定我们的人品足够好，不考虑冲突情况。
我们可以通过前缀的哈希计算出子串的哈希。
哈希表4
计算过程：

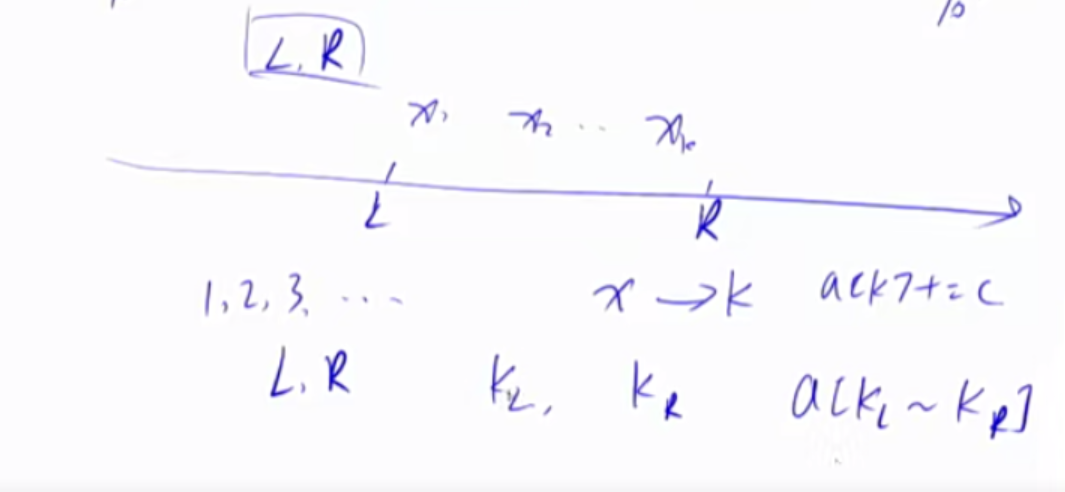
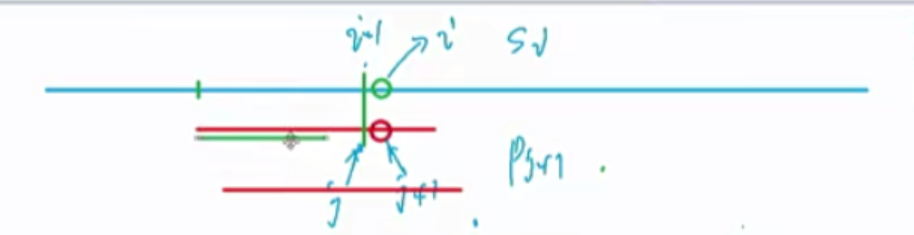
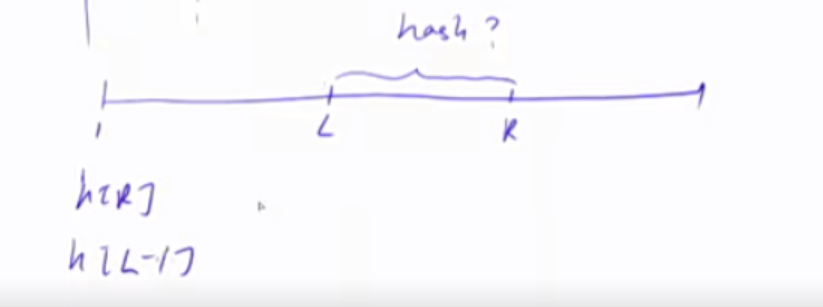
1) 把H[L-1]这一段向右平移到和H[R]对齐的位置。即$H[L-1]\times P^{R-L+1}$
2) $hash[L-R] = H[R]-H[L-1]\times P^{R-L+1}$

由上式可得，对于一个区间长度为1的区间来说，L = R，str(i) = H(i)-H(i-1)P,因此在计算前缀和的hash时，H(i) = H(i-1)\P+str(i)。
例题：
哈希表5

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
核心思想：将字符串看成P进制数，P的经验值是131或13331，取这两个值的冲突概率低
小技巧：取模的数用2^64，这样直接用unsigned long long存储，溢出的结果就是取模的结果

typedef unsigned long long ULL;
ULL h[N], p[N]; // h[k]存储字符串前k个字母的哈希值, p[k]存储 P^k mod 2^64

// 初始化
p[0] = 1;
for (int i = 1; i <= n; i ++ )
{
    h[i] = h[i - 1] * P + str[i];
    p[i] = p[i - 1] * P;
}

// 计算子串 str[l ~ r] 的哈希值
ULL get(int l, int r)
{
    return h[r] - h[l - 1] * p[r - l + 1];
}

例题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<iostream>

using namespace std;

using ULL = unsigned long long;

const int N = 100010,P = 131;

int n,m;
char str[N];
ULL h[N],p[N];

UUL get(int l,int r){
    return h[r]-h[l-1]*p[r-l+1];
}

int main(){
    scanf("%d%d%s",&n,&m,str+1);

    p[0] = 1;
    for(int i = 1;i<=n;i++){
        p[i] = p[i-1]*p;//预处理出p的i次方的值
        h[i] = h[i-1]*p+str[i];
    }

    while(m--){
        int l1,r1,l2,r2;
        scanf("%d%d%d%d",&l1,&r1,&l2,&r2);

        if(get(l1,r1) == get(l2,r2)){
            cout<<"Yes"<<endl;
        }else{
            cout<<"No"<<endl;
        }
    }
}

KMP可以用来求字符串的循环节，但是hash不可以。其他的功能hash都可以代替KMP。
01：12：17

C++ STL

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
vector, 变长数组，倍增的思想：当系统为某一个程序分配空间的时候，所需时间，与空间大小无关，与请求次数有关。例如，最开始先给vector分配一个32的空间，当不够用的时候，下一次申请的空间大小为64，并将32内的数据copy到64中去。
    size()  返回元素个数,所有容器都有
    empty()  返回是否为空，所有容器都有
    clear()  清空，并不是所有容器都有，queue就没有
    front()/back()
    push_back()/pop_back()
    begin()/end()
    []支持随机寻址
    使用迭代器来遍历
    for(vector<int>::iterator i = a.begin();i!=a.end();i++) cout<<*i<<endl
    for(auto x:a) cout<<x<<endl;
    支持比较运算，按字典序
    vector<int>a(4,3),b(3,4);
    if(a<b){
        cout<<"a<b"<<endl;
    }

pair<int, int> 可以存储一个二元组，相当于C++定义的一个结构体，自带一个比较函数
    first, 第一个元素
    second, 第二个元素
    支持比较运算，以first为第一关键字，以second为第二关键字（字典序）
    pair<int,string>p;
    p = make_pair(10,"kongming");
    p = (20,"abc");
    //当需要三元组的时候，需要如下格式
    pair<int,pair<int ,int>>p;

string，字符串
    size()/length()  返回字符串长度
    empty()
    clear()
    substr(起始下标，(子串长度))  返回子串，当子串长度大于字符串长度时，会返回到字符串结尾。字串长度是可选参数，默认值是字符串结尾。
    cout<<a.substr(1,2)<<endl;
    c_str()  返回字符串所在字符数组的起始地址,在使用printf函数输出字符串时用得到。
    printf("%s\n",a.c_str());
    重载了+运算符，可以支持两个字符串相加，或是一个字符串和一个字符相加。

queue, 队列,没有claer()函数
    #include<queue>
    如果想要清空queue，只需要重新构造一个queue
    q = queue<int>();
    size()
    empty()
    push()  向队尾插入一个元素
    front()  返回队头元素
    back()  返回队尾元素
    pop()  弹出队头元素

priority_queue, 优先队列，默认是大根堆,没有clear函数
    size()
    empty()
    push()  插入一个元素
    top()  返回堆顶元素
    pop()  弹出堆顶元素
    默认是大根堆，我们如果需要小根堆，可以每次向优先队列中插入-x。
    定义成小根堆的方式：priority_queue<int, vector<int>, greater<int>> q;

stack, 栈
    size()
    empty()
    push()  向栈顶插入一个元素
    top()  返回栈顶元素
    pop()  弹出栈顶元素

deque, 双端队列,队头和队尾都可以插入删除，还可以支持随机访问，是一个加强版的vector，速度稍慢一点
    size()
    empty()
    clear()
    front()/back()
    push_back()/pop_back()
    push_front()/pop_front()
    begin()/end()//支持begin、end迭代器
    []

set, map, multiset, multimap, 基于平衡二叉树（红黑树），动态维护有序序列
    如果在set中插入重复元素，这个操作将会被忽略。
    size()
    empty()
    clear()
    begin()/end()
    迭代器支持++, -- 返回前驱和后继，时间复杂度 O(logn)

    set/multiset
        insert()  插入一个数 logn的复杂度
        find()  查找一个数
        count()  返回某一个数的个数
        erase()
            (1) 输入是一个数x，删除所有x   O(k + logn) k是x的个数
            (2) 输入一个迭代器，删除这个迭代器
        lower_bound()/upper_bound() //set核心操作
            lower_bound(x)  返回大于等于x的最小的数的迭代器 这个包括x
            upper_bound(x)  返回大于x的最小的数的迭代器 这个不包括x
    map/multimap，除了size，empty之外，其他操作包括 ++ --操作复杂度都是logn。
        insert()  插入的数是一个pair，map可以像数组那种对一个键值对赋值，访问也可以用数组方式。
        erase()  输入的参数是pair或者迭代器
        find()
        []  注意multimap不支持此操作。 时间复杂度是 O(logn)
        lower_bound()/upper_bound()

unordered_set, unordered_map, unordered_multiset, unordered_multimap, 哈希表
    #include<unordered_map>
    和上面类似，增删改查的时间复杂度是 O(1)
    不支持 lower_bound()/upper_bound()， 迭代器的++，--，因为内部是无序的。

bitset, 压位
    C++里面的bool类型的大小是一个字节。如果我们需要1024个bool类型的变量，就需要1024*8bit，但是如果我们使用1bit来记录一个bool值，就只需要1024bit。
    bitset<10000> s;//定义长度为10000个bit
    ~, &, |, ^ //取反、与、或、异或
    >>, <<//移位
    ==, !=
    [] //支持数组访问

    count()  返回有多少个1

    any()  判断是否至少有一个1
    none()  判断是否全为0

    set()  把所有位置成1
    set(k, v)  将第k位变成v
    reset()  把所有位变成0
    flip()  等价于~
    flip(k) 把第k位取反

具体使用：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<vector>

using namespace std;

//定义一个长度为10的vector
vector<int>a(10);
//定义一个长度为10的vector，且里面的每一个数都是3
vector<int>a(10,3);
//定义一个vector数组
vector<int>a[10];

07

树与图的遍历

树与图的遍历1
DFS 回溯+剪枝
树与图的遍历2
DFS最重要的就是要考虑好顺序。
树与图的遍历3
虽然DFS看起来是一棵树，但是我们在存储的时候，只存储当前的路径。
在进行回溯操作的时候，一定要记得恢复现场。
树与图的遍历4
思路一，枚举每一个皇后能放到哪一行。在放完最后一个皇后之后判断是否满足题目要求。也可以在放置皇后的过程中，不断判断有没有冲突

1
2
3
4
5
6
7
8
9
10
int dfs(int u)
{
    st[u] = true; // st[u] 表示点u已经被遍历过

    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j]) dfs(j);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include<iostream>
using namespace std;
const int N = 10;
int n;
int path[N];
bool st[N];
void dfs(int u){
    if(u == n){//当已经填满了所有空位时
        for(int i = 0;i<n;i++){
            cout<<path[i]<<" ";
            return;
        }
    }
    for(int i = 1;i<=n;i++){
        if(!st[i]){//寻找没有被访问过的数
            path[u] = i;//记录路径
            st[i] = true;//表示i已经被用过
            dfs(u+1);
            st[i] = false;//恢复现场
        }
    }
}
int main(){
    cin>>n;
    dfs(0);
    return 0;
}

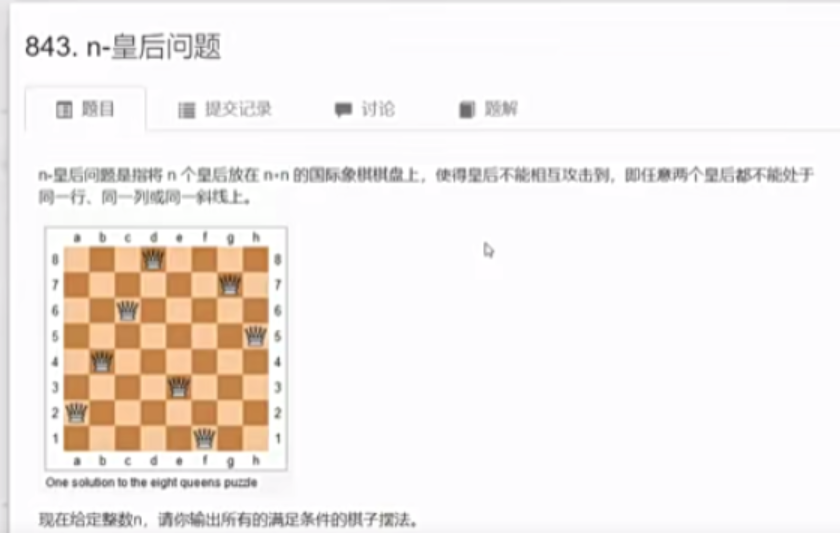
n皇后问题思路二：对每个格子进行dfs，有放下和不放下两种选择，放下的时候要注意检查是否满足条件。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<iostream>
const int N = 20;
int n;
char g[N][N];
bool col[N],dg[N],udg[N],row[N];

void dfs(int x,int y,int s){
    if(y == n){
        y = 0;
        x++;
    }
    if(x == n){//如果此时已经遍历到最后一行
        if(s == n){
            for(int i = 0;i<n;i++){
                cout<<g[i];
            }
            cout<<endl;
        }
        return;
    }

    //不放皇后
    dfs(x,y+1,s);

    //放皇后
    //对角线从左上角和右上角进行编号，它与x和y的关系可以根据二次函数来决定
    if(!row[x]&&!col[y]&&!dg[x+y]&&!udg[x-y+n]){
        g[x][y] = 'Q';
        row[x] = col[y] = dg[x+y] = udg[x-y+n] = true;
        dfs(x,y+1,s+1);
        row[x] = col[y] = dg[x+y] = udg[x-y+n] = false;
        g[x][y] = '.';//在使用的时候，注意要将g数组中的内容初始化为.
    }
}

00:55:07
BFS
树与图的遍历5
树与图的遍历6

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
queue<int> q;
st[1] = true; // 表示1号点已经被遍历过
q.push(1);

while (q.size())
{
    int t = q.front();
    q.pop();

    for (int i = h[t]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j])
        {
            st[j] = true; // 表示点j已经被遍历过
            q.push(j);
        }
    }
}

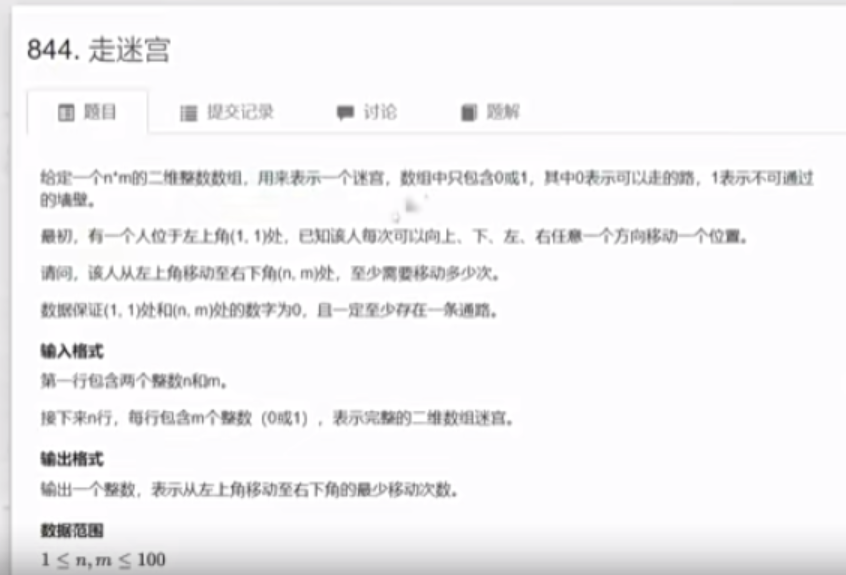
BFS例题答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include<iostream>
#include<algorithm>
#include<queue>
#include<cstring>

using namespace std;

using PII = pari<int ,int>;

const int N = 110;
//g数组存的是地图，d数组存的是每个点到起点的距离
int n，m
int g[N][N];
int d[N][N];
PII prev[N][N];//记录路径
queue<int> q;

int BFS(){
    PII start = {0,0};
    q.push(start);

    memset(d,-1,sizeof(d));
    d[0][0] = 0;

    int dx[4] = {-1,0,1,0},dy[4] = {0,1,0,-1};

    while(!q.empty()){
        auto t = q.top();
        q.pop();
        for(int i = 0;i<4;i++){
            int x = t.first+dx[i],y = t.second+dy[i];
            if(x>=0&&x<n&&y>=0&&y<m&&g[x][y] == 0&&d[x][y]!=-1){
                d[x][y] = d[t.first][t.second]+1;
                prev[x][y] = t; 
                q.push({x,y});
            }
        }
    }
    int x = n-1,y = m-1;
    while(x||y){
        cout<<x<<" "<<y<<endl;
        auto t = prev[x][y];
        x = t.first,y = t.second;
    }
    return d[n-1][m-1];
}

int main(){
    cin>>n>>m;
    for(int i = 0;i<n;i++){
        for(int j = 0;j<n;j++){
            cin>>g[i][j];
        }
    }
    cout<<BFS()<<endl;
}

01:17:08

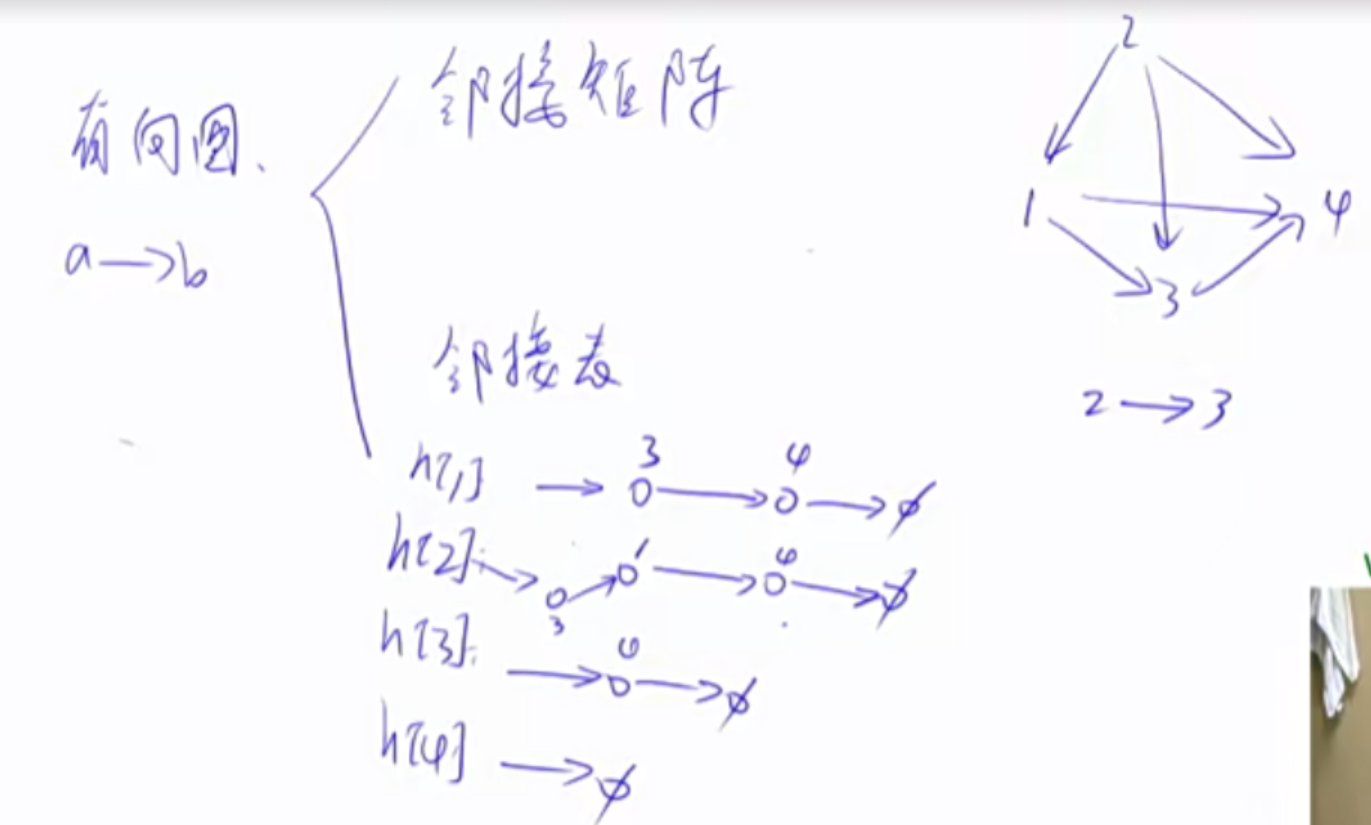
树与图的存储

树是特殊的图。树是无环连通图。因此我们只会探讨图。图分为有向图和无向图。无向图是一种特殊的有向图。要存储一个无向图ab，则需要建立两条边，a->b和b->a。
有向图的存储方法一般为两种：
1)邻接矩阵。g[a,b]表示a到b这条边的信息。
2)邻接表。
树与图的存储1
树的重心

1
2
3
4
5
6
7
8
9
10
11
12
// 对于每个点k，开一个单链表，存储k所有可以走到的点。h[k]存储这个单链表的头结点
int h[N], e[N], ne[N], idx;

// 添加一条边a->b
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

// 初始化
idx = 0;
memset(h, -1, sizeof h);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include<iostream>
#include<cstring>
#include<algorithm>

const int N = 100010,M = N/2;
int ans = N;
int st[N];

//h存储的是N个节点的链表头，e存的链表上节点的值，ne存的是链表节点的next指针
int h[N],e[M],idx;

//插入由a指向b的边
void add(int a,int b){
    e[idx] = b,ne[idx] = h[a],h[a] = idx++;
}

int dfs(int u)
{
    st[u] = true; // st[u] 表示点u已经被遍历过

    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j]) dfs(j);
    }
}

int main(){
    //链表的初始化
    memset(h,-1,sizeof h);
    cin>>n;

    for(int i = 0;i<n-1;i++){
        int a,b;
        cin>>a>>b;
        //因为是无向边所以需要加入两条边
        add(a,b),add(b,a);
    }
    dfs(1);
    cout<<ans<<endl;
    return 0;
}

例题的答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//以u为根的子树中点的数量
int dfs(int u){
    st[u] = true;//标记u节点已经被访问过了

    int sum = 1;//u节点也算是一个点
    int res = 0;
    for(int i = h[u];i!=-1;i = ne[i]){
        int j = e[i];
        if(!st[j]){
            int s= dfs(j);
            res = max(res,s);
            sum = s+sum;
        }
    }
    res = max(res,n-sum);
    ans = min(ans,res);
    return sum;
}

01:47:05
BFS算法
“所有边的长度为1”就暗示着可以用bfs来求解最短路。
题目如下：
树与图的存储2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 100010;

int n,m;
int h[N],e[N],ne[N],idx;
//d是距离，q是队列
int d[N],q[N];
int main(){
    cin>>n>>m;
    memset(h,-1,sizeof h);
    for(int i = )
}

图的bfs例题。
利用bfs求距离。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;
const int N = 100010;

int n, m;
int h[N], e[N], ne[N], idx;
int d[N], q[N];
void add(int a, int b) {
 e[idx] = b;
 ne[idx] = h[a];
 h[a] = idx++;
}
int bfs() {
 int hh = 0, tt = 0;
 q[0] = 1;

 memset(d, -1, sizeof d);

 //queue is not null
 while (hh <= tt) {
  int t = q[hh++];
  for (int i = h[t]; i != -1; i = ne[i]) {
   int j = e[i];
   if (d[j] == -1) {
    d[j] = d[t] + 1;
    q[++t] = j;
   }
  }
 }
 return d[n];
}
int main() {
 cin >> n >> m;
 memset(h, -1, sizeof h);
 for (int i = 0; i < m; i++) {
  int a, b;
  cin >> a >> b;
  add(a, b);
 }
 cout << bfs() << endl;
 return 0;
}

图的bfs的经典应用就是求拓扑序。
有向图的拓扑序列。
特点：从起点出发指向终点，完成事情的顺序。
有环的情况下就不存在拓扑序。可以证明，一个有向无环图一定存在拓扑序。因此，有向无环图也可以称为拓扑图。
度数：
树与图的存储3
当前入度为0的点都是可以作为起点的。因此拓扑排序的第一步就是把所有入度为0的点入队，例如此时队头元素为t。然后枚举t的所有出边，t->j。删掉t，意味着此时条件t已经被满足，从而影响了j的入度，j的入度dj需要减一。如果此时dj==0，那么就让j入队。
树与图的存储4
一个无环图，一定至少存在一个入度为0的点。
一个有向无环的拓扑序是不唯一的。
bfs思想实现拓扑排序代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;

const int N = 100010;
int n, m;
int h[N], e[N], ne[N], idx;
int q[N], d[N];
//d指的是d的度
void add(int a, int b) {
 e[idx] = b;
 ne[idx] = h[a];
 h[a] = idx++;
}
bool topsort() {
 int hh = 0, tt = -1;
 for (int i = 1; i <= n; i++) {
  if (!d[i]) {
   q[++t] = i;
  }
 }
 while (hh <= tt) {
  int t = q[hh++];
  //出队的顺序就是拓扑序
  for (int i = h[t]; i != -1; i = ne[i]) {
   int j = e[i];
   d[j]--;
   if (d[j] == 0) {
    q[++tt] = j;
   }
  }
 }
 return tt == n-1//所有点都进入队列
}
int main() {
 cin >> n >> m;
 memset(h, -1, sizeof h);
 for (int i = 0; i < m; i++) {
  int a, b;
  cin >> a >> b;
  add(a, b);
  d[b]++;
 }
 if (topsort()) {
  for (int i = 0; i < n; i++) {
   cout << q[i] << " ";
  }
 }
 else {
  cout << -1 << endl;
 }
 return 0;
}

拓扑排序要注意的是，条件是头节点，计算的度数是被条件限制的对象。

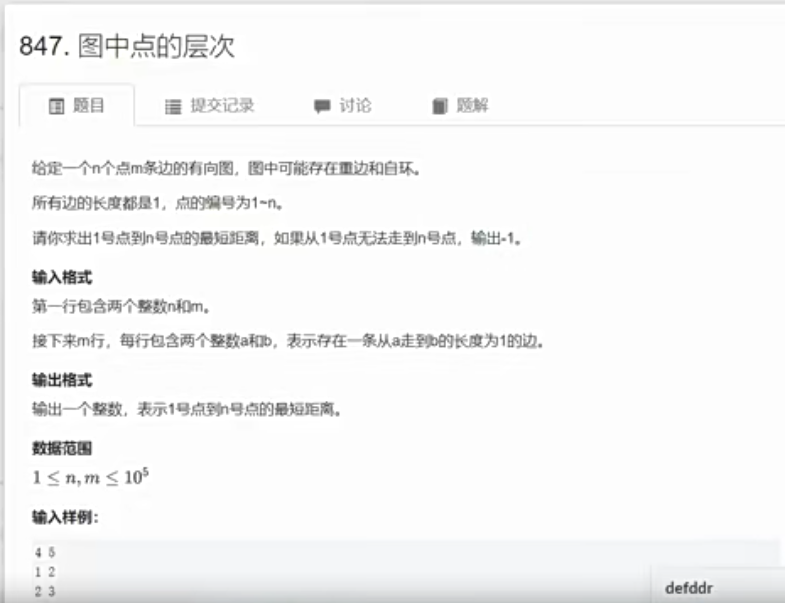
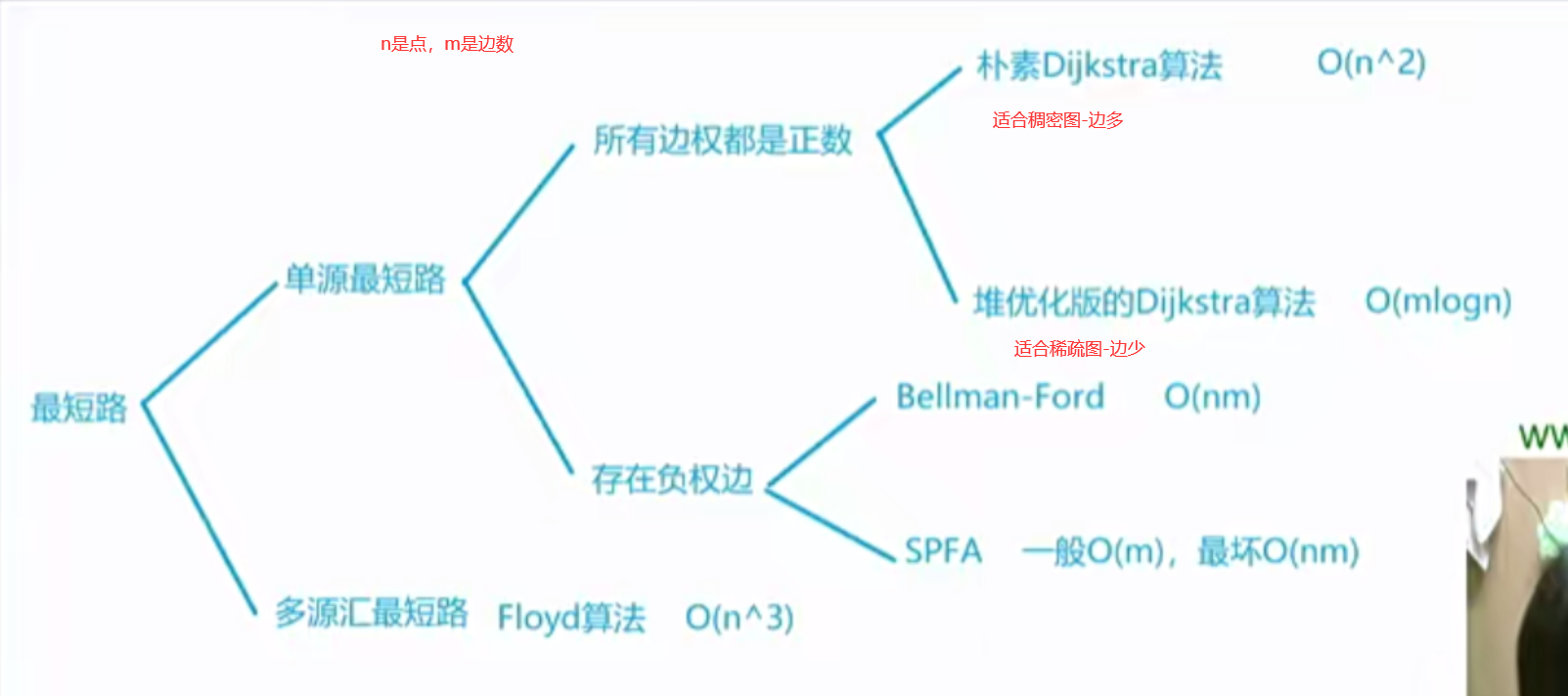
朴素dijkstra算法

最短路问题通常分为两类。
1)单源最短路。求一个点到所有点的最短距离。稠密图边数m是点数n方级别的。
2)多源汇最短路。源指的是起点，汇点指的是终点。
朴素dijkstra算法1
不超过k条边用BF比较好。
朴素dijkstra算法2
先初始化距离，dis1=0，其余是正无穷。然后找出不在s中距离最近的点q，将q点加入集合s中，确定q的最短距离，并用q来更新dis数组。
两层循环，复杂度是n^2的。
稠密图用邻接矩阵来存储，稀疏图用邻接表来存储。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int g[N][N];  // 存储每条边
int dist[N];  // 存储1号点到每个点的最短距离
bool st[N];   // 存储每个点的最短路是否已经确定

// 求1号点到n号点的最短路，如果不存在则返回-1
int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    for (int i = 0; i < n - 1; i ++ )
    {
        int t = -1;     // 在还未确定最短路的点中，寻找距离最小的点
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;

        // 用t更新其他点的距离
        for (int j = 1; j <= n; j ++ )
            dist[j] = min(dist[j], dist[t] + g[t][j]);

        st[t] = true;
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 510;

int n,m;
int g[N][N];
int dist[N];//表示当前的最短距离是多少
bool st[N];//表示对应点的最短距离是否已经确定

int dijkstra(){
    memset(dist,0x3f,sizeof dist);
    dist[1] = 0;

    for(int i = 0;i<n;i++){
        int t = -1;
        for(int j = 1;i<=n;j++){
            if((!st[j])&&(t == -1||dist[t]>dist[j])){
                t = j;
            }
        }
        if(t == n) break;
        st[t] = true;
        for(int j = 1;j<=n;j++){
            dist[j] = min(dist[j],dist[t]+g[t][j]);
        }
    }
    if(dist[n] == 0x3f3f3f3f){
        return -1;
    }else{
        return dist[n];
    }
}

int main(){
    scanf("%d%d",&m,&n);

    memset(g,0x3f,sizeof g);

    while(m--){
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        g[a][b] = min(g[a][b],c);//在有重边的情况下，选择w较小的那条边。
    }

    int t = dijkstra();

    printf("%d\n",t);
    return 0;
}

堆优化的dijkstra算法

堆有两种实现方式，第一种是手写堆(前面有讲过),第二种方式是使用优先队列。priority_queue。
优先队列不支持修改堆中元素，因此队列中的元素个数多于node个。
稀疏图，将存储方式改成邻接表的形式。
类似于宽搜。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

using pair<int,int> = PII;

const int N = 100010;

int n,m;
int h[N],w[N],e[N],ne[N],idx;
int dist[N];//表示当前的最短距离是多少
bool st[N];//表示对应点的最短距离是否已经确定

void add(int a,int b,int c){
    e[idx] = b;
    w[idx] = c;
    ne[idx] = h[a]
    h[a] = idx++;
}

int dijkstra(){
    memset(dist,0x3f,sizeof dist);
    dist[1] = 0;
    priority_queue<PII,vector<PII>,greater<PII>> heap;//小根堆
    heap.push({0,1});//距离是0，编号是1

    while(heap.size()){
        auto t = heap.top();
        heap.pop();

        int ver = t.second(),distance = t.first();//貌似不用加括号
        if(st[ver]) continue;

        for(int i = h[ver];i!=-1;i = ne[i]){
            int j = e[i];
            if(dist[j]>dist[t]+w[i]){
                dist[j] = distance+w[i];
                heap.push({dist[j],j});
            }
        }
    }

    if(dist[n] == 0x3f3f3f3f){
        return -1;
    }else{
        return dist[n];
    }
}

int main(){
    scanf("%d%d",&m,&n);

    memset(h,-1,sizeof h);

    while(m--){
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c);//重边无所谓
    }

    int t = dijkstra();

    printf("%d\n",t);
    return 0;
}

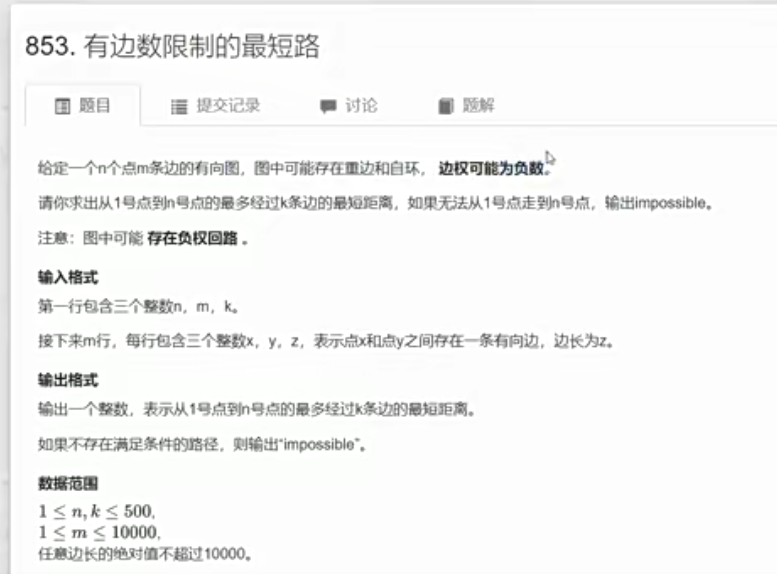
Bellman-Ford算法

BF算法存边直接定义一个结构体，a，b，w就可以，不需要邻接表，临界矩阵。
Bellman-Ford算法1
BF算法运行完毕后保证dist[b]<=dist[a]+w。BF更新的过程叫松弛操作。
BF算法用于处理有负权边的问题，但是有负权回路时，最短路不一定存在。可以用BF算法求解图中是否有负权回路。
算法迭代k次的意义在于：求从1号点，经过不超过k条边，所得到的最短距离。如果迭代n次，还会更新点，就说明存在边数为n的最短路径，也就是存在负环。
算法时间复杂度，n次，m个边，O(nm)。
适用于有边数限制的最短路径。
当负环不在a和b之间时，不影响使用BF算法求解最短路径，但是SPFA算法要求图中一定不能有负环。

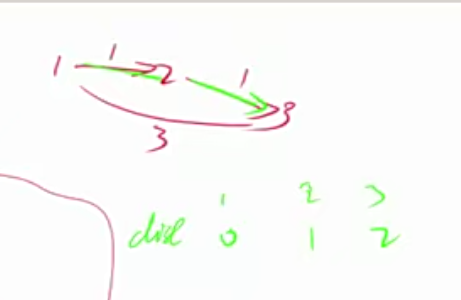
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
int n, m;       // n表示点数，m表示边数
int dist[N];        // dist[x]存储1到x的最短路距离

struct Edge     // 边，a表示出点，b表示入点，w表示边的权重
{
    int a, b, w;
}edges[M];

// 求1到n的最短路距离，如果无法从1走到n，则返回-1。
int bellman_ford()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    // 如果第n次迭代仍然会松弛三角不等式，就说明存在一条长度是n+1的最短路径，由抽屉原理，路径中至少存在两个相同的点，说明图中存在负权回路。
    for (int i = 0; i < n; i ++ )
    {
        for (int j = 0; j < m; j ++ )
        {
            int a = edges[j].a, b = edges[j].b, w = edges[j].w;
            if (dist[b] > dist[a] + w)
                dist[b] = dist[a] + w;
        }
    }

    if (dist[n] > 0x3f3f3f3f / 2) return -1;
    return dist[n];
}

例题。
Bellman-Ford算法2
当限制了经过的边的个数，那么有负环就无所谓了。
Bellman-Ford算法3
上图表示了BF算法更新过程中出现串联的结果，如果k = 1，那么在第一轮算法更新中，我们用第一条边dist2 = 1，然后再用第二条边，dist3 = 2(因为此时dist2已经更新过了),所以为了避免不符合dist中边数的限制，我们在本轮更新中，只使用上一轮得到的结果，即使用的是上一轮的备份，这也是我们需要在i每次更新前对dist数组进行备份的原因。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 510,M = 100010;

int n,m;
int dist[N],backcup[N];

struct Edge{
    int a,b,w;
}edges[M];

int bellman_ford(){
    memset(dist, 0x3f, sizeof dist);//不要忘记初始化
    dist[1] = 0;
    for(int i = 0;i<k;i++){
        memcpy(backup,dist,sizeof dist);
        for(int j = 0;j<m;j++){
            int a = edges[j].a,b = edges[j].b,w = edges[j].w;
            dist[b] = min(dist[b],backup[a]+w);//注意这里不是dist[a]
        }
    }
    if(dist[n]>0x3f3f3f3f/2){
        return -1;
    }
}

int main(){
    scanf("%d%d%d",&m,&n,&k);

    for(int i = 0;i<m;i++){
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        edges[i] = {a,b,w};
    }

    int t = bellman_ford();
    if(t == -1){
        cout<<"impossible"<<endl;
    }else{
        cout<<t<<endl;
    }

    return 0;
}

spfa 算法（队列优化的Bellman-Ford算法）

只有a变小了，b才会变小，因此我们用一个队列，专门来存储变小过的a，然后以此为根据来更新变小的b。
spfa算法1
spfa算法伪代码如下：
spfa算法2
queue中的点就是待更新的点。只有前面的a点变小了，后面的点才有可能会需要更新。不一定要用队列，也可以用堆等等，一般用队列。
非常类似于dijkstra。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
int n;      // 总点数
int h[N], w[N], e[N], ne[N], idx;       // 邻接表存储所有边
int dist[N];        // 存储每个点到1号点的最短距离
bool st[N];     // 存储每个点是否在队列中

// 求1号点到n号点的最短路距离，如果从1号点无法走到n号点则返回-1
int spfa()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    queue<int> q;
    q.push(1);
    st[1] = true;

    while (q.size())
    {
        auto t = q.front();
        q.pop();

        st[t] = false;

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                if (!st[j])     // 如果队列中已存在j，则不需要将j重复插入
                {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

关键改动。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
cnt[N];
int spfa(){
    memset(dist,0x3f,sizeof dist);
    dist[1] = 0;
    queue<int>q;
    q.push(1);//求dist时用这个
    //判负环用这个，需要把所有点全部加入queue中
    for(int i = 1;i<=n;i++){
        st[i] = true;
        q.push(i);
    }
    st[1] = true;//st数组存的是当前这个点是否在队列中，防止队列中存重复的点
    while(q.size()){
        int t = q.front();
        q.pop();

        st[t] = false;

        for(int i = h[t];i!=-1;i = ne[i]){
            int j = e[i];
            if(dist[j]>dist[t]+w[i]){
                dist[j] = dist[t]+w[i];
                cnt[j] = cnt[t]+1;//判负环用
                if(cnt[j]>=n){
                    return true;//判负环用
                }
                if(!st[j]){
                    q.push(j);
                    st[j] = true; 
                }
            }
        }
    }
    //spfa求dist
    if(dist[n] == 0x3f3f3f3f) return -1;
    else return dist[n];
    //spfa判负环
    return false;
}

spfa判断图中是否存在负环。原理是抽屉原理。
dist[x]表示的是1到x的最短距离。
cnt[x]表示的是边数。
更新方式如下图：
spfa算法3
如果cnt[x]>=n,就意味着从1到x至少经过了n条边，也就意味着经过了n+1个点，也就意味着存在两个点的值是相同的。也就意味着路径中存在一个环。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
int n;      // 总点数
int h[N], w[N], e[N], ne[N], idx;       // 邻接表存储所有边
int dist[N], cnt[N];        // dist[x]存储1号点到x的最短距离，cnt[x]存储1到x的最短路中经过的点数
bool st[N];     // 存储每个点是否在队列中

// 如果存在负环，则返回true，否则返回false。
bool spfa()
{
    // 不需要初始化dist数组
    // 原理：如果某条最短路径上有n个点（除了自己），那么加上自己之后一共有n+1个点，由抽屉原理一定有两个点相同，所以存在环。

    queue<int> q;
    for (int i = 1; i <= n; i ++ )
    {
        q.push(i);
        st[i] = true;
    }

    while (q.size())
    {
        auto t = q.front();
        q.pop();

        st[t] = false;

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                cnt[j] = cnt[t] + 1;
                if (cnt[j] >= n) return true;       // 如果从1号点到x的最短路中包含至少n个点（不包括自己），则说明存在环
                if (!st[j])
                {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }

    return false;
}

在实现过程中注意h的初始化，ne的初始化，idx的初始化，cnt的初始化，dist的初始化，vt的初始化。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include<iostream>
#include<cstring>
#include<queue>
#define N 2020
#define num_dege 6010
using namespace std;
queue<int>que;
int vt[N], dist[N];
int T;
int h[N], e[num_dege], ne[num_dege], w[num_dege],idx;
int cnt[num_dege];
int n, m;
void add(int a, int b, int w) {
 e[idx] = b;
 ::w[idx] = w;
 ne[idx] = h[a];
 h[a] = idx++;
}
bool spfa() {
 memset(dist, 0x3f, sizeof dist);
 vt[1] = true;
 dist[1] = 0;
 que.push(1);
 while (!que.empty()) {
  int t = que.front();
  que.pop();
  vt[t] = 0;
  for (int i = h[t]; i != -1; i = ne[i]) {
   int j = e[i];
   if (dist[j] > dist[t] + w[i]) {
    dist[j] = dist[t] + w[i];
    cnt[j] = cnt[t] + 1;
    if (cnt[j] >= n) {
     return true;
    }
    if (!vt[j]) {
     que.push(j);
     vt[j] = true;
    }
   }
  }
 }
 return false;
}
int main() {
 cin >> T;
 while (T--) {
  memset(ne, -1, sizeof ne);
  memset(h, -1, sizeof h);
  memset(vt, 0, sizeof vt);
  memset(cnt, 0, sizeof cnt);
  idx = 0;
  cin >> n >> m;
  int a, b, w;
  for (int i = 0; i < m; i++) {
   cin >> a >> b >> w;
   if (w >= 0) {
    add(a, b, w);
    add(b, a, w);
   }
   else {
    add(a, b, w);
   }
  }
  if (spfa()) {
   cout << "YES\n";
  }
  else {
   cout << "NO\n";
  }
 }
 return 0;
}

floyd算法

Floyd是多源汇最短路。邻接矩阵存储所有的边。三重循环。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
初始化：
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= n; j ++ )
            if (i == j) d[i][j] = 0;
            else d[i][j] = INF;

// 算法结束后，d[a][b]表示a到b的最短距离
void floyd()
{
    for (int k = 1; k <= n; k ++ )
        for (int i = 1; i <= n; i ++ )
            for (int j = 1; j <= n; j ++ )
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}

原理：三维状态表示d[k,i,j]只经过1-k这些中间点，从i到达j的最短距离。d[k,i,j] = d[k-1,i,k]+d[k-1,k,j]。我们发现第一维可以去掉。
例题如下：
Floyd算法1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include<cstring>
#include<iostream>
#include<algorithm>

using namespace std;

const int N = 210,INF = 1e9;
//有重边和自环

int n,m,Q;
ind d[N][N];

void floyd(){
    for(int k = 1;k<=n;k++){
        for(int i = 1;i<=n;i++){
            for(int j = 1;j<=n;j++){
                d[i][j] = min(d[i][j],d[i][k]+d[k][j])
            }
        }
    }
}

int main(){
    scanf("%d %d %d",&n,&m,&Q);

    for(int i = 1;i<=n;i++){
        for(int j = 1;j<=n;j++){
            if(i == j)d[i][j] = 0;
            else d[i][j] = INF;
        }
    }

    while(m--){
        int a,b,w;
        scanf("%d%d%d",&a,&b,&w);

        d[a][b] = min(d[a][b],w);
    }

    floyd();

    while(Q--){
        int a,b;
        scanf("%d%d",&a,&b);
        if(d[a][b] > INF/2) cout<<"impossible"<<endl;//可能存在一些负权边
        else printf("%d",d[a][b]);
    }
    return 0;
}

朴素版prim算法

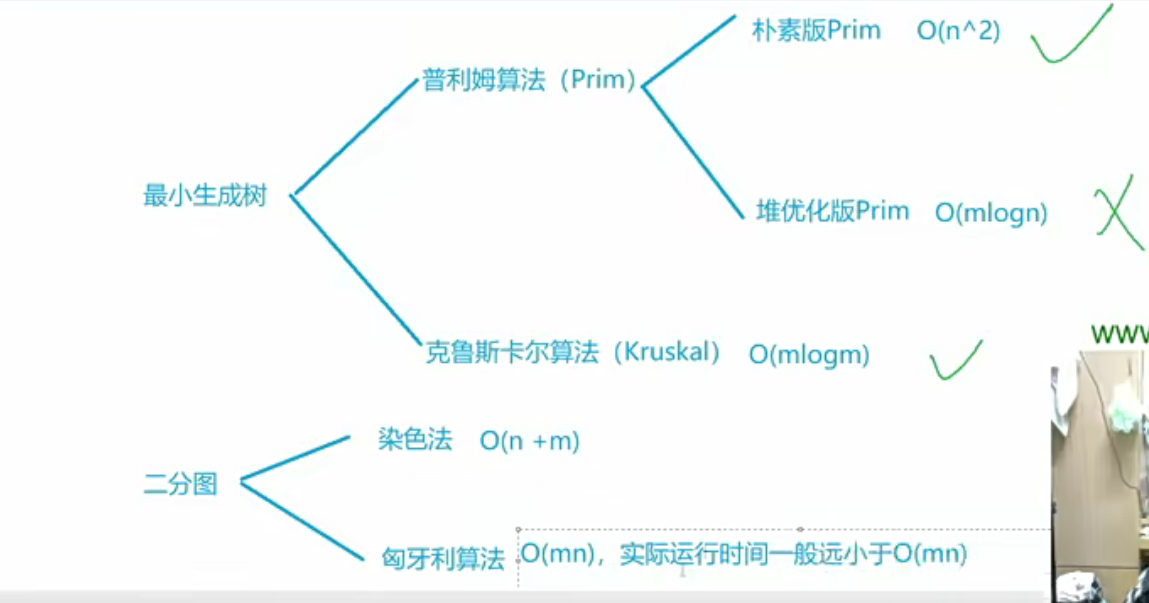
朴素版prim算法1
最小生成树对应的是无向图。
如果是稠密图则使用朴素版的Prim算法，如果是稀疏图，则使用kruskal算法。堆优化版本的prim算法不常用。
染色法就是DFS。匈牙利算法用于求解二分图的最大匹配。
prim算法类似于dijkstra。
算法思路如下：
朴素版prim算法2
A点所有连向集合内部中点的边的最小值，称为点到集合的距离。在生成树中选择的边就是这个最小距离。
在最小生成树的问题中，边的正负都没有问题。
集合指的是当前已经在连通块中的所有点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
int n;      // n表示点数
int g[N][N];        // 邻接矩阵，存储所有边
int dist[N];        // 存储其他点到当前最小生成树的距离
bool st[N];     // 存储每个点是否已经在生成树中


// 如果图不连通，则返回INF(值是0x3f3f3f3f), 否则返回最小生成树的树边权重之和
int prim()
{
    memset(dist, 0x3f, sizeof dist);

    int res = 0;
    for (int i = 0; i < n; i ++ )
    {
        int t = -1;
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;

        if (i && dist[t] == INF) return INF;

        if (i) res += dist[t];
        st[t] = true;

        for (int j = 1; j <= n; j ++ ) dist[j] = min(dist[j], g[t][j]);
    }

    return res;
}

cost先累加，再更新。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 530,INF = 0x3f3f3f3f;

//稠密图 邻接矩阵

int n,m;
int g[N][N];
int dist[N];
//dist表示点到连通块的距离
bool st[N];

int prim(){
    memset(dist,0x3f,sizeof dist);

    int res = 0;
    for(int i = 0;i<n;i++){
        int t = -1;
        for(int j = 1;j<=n;j++){
            if(!st[j]&&(t == -1||dist[t]>dist[j])){//找出目前最小的dist
                t = j;
            }
        }
        if(i&&dist[t] == INF){//如果不是第一个点且到t的距离是正无穷，则图是不连通的
            return INF; 
        }
        if(i){//只要不是第一条边，就把dist加入到答案中去
            res += dist[t];
        }
        //当图中有自环时，当选中t时，如果t是一个负环，那么在下一步更新中t就会更新自己的dist[t]来让它变得更小，而根据定义，最小生成树中是没有环的，因此要在更新之前记录cost.

        for(int j = 1;j<n;j++){
            dist[j] = min(dist[j],g[t][j])
        }

        st[t] = true;//将这个点加入到集合中去
    }
    return res;
}

//可能有重边
int main(){
    scanf("%d %d",&m,&n);

    memset(g,0x3f sizeof g);

    while(m--){
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        g[a][b] = g[b][a] = min(g[a][b],c);
    }

    int t = prim();

    if(t == INF) cout<<"不存在生成树";
    else cout<<t;
}

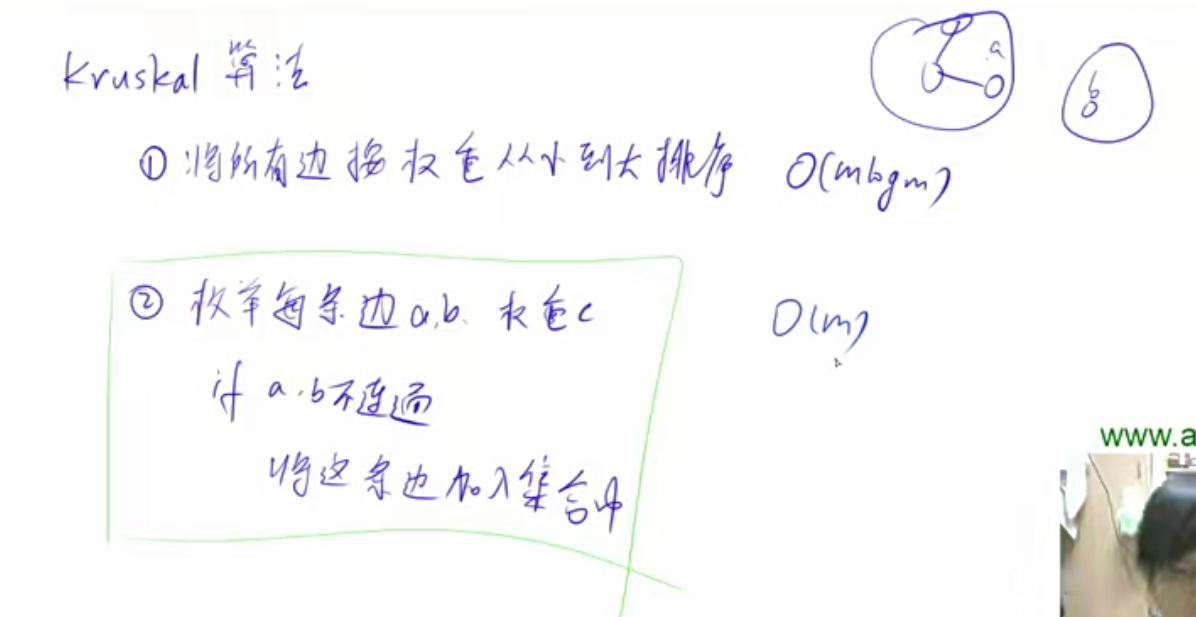
Kruskal算法

算法思路如下：
Kruskal算法1
特点：不需要特殊的方式存图，只需要简单开个结构体就可以。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
int n, m;       // n是点数，m是边数
int p[N];       // 并查集的父节点数组

struct Edge     // 存储边
{
    int a, b, w;

    bool operator< (const Edge &W)const
    {
        return w < W.w;
    }
}edges[M];

int find(int x)     // 并查集核心操作
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int kruskal()
{
    sort(edges, edges + m);

    for (int i = 1; i <= n; i ++ ) p[i] = i;    // 初始化并查集

    int res = 0, cnt = 0;
    for (int i = 0; i < m; i ++ )
    {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;

        a = find(a), b = find(b);
        if (a != b)     // 如果两个连通块不连通，则将这两个连通块合并
        {
            p[a] = b;
            res += w;
            cnt ++ ;
        }
    }

    if (cnt < n - 1) return INF;
    return res;
}

例题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include<iostream>
#include<algorithm>
using namespace std;

const int N = 200010;

int n,m;
int p[N];

struct Edge{
    int a,b,w;
    //重载小于号，方便排序,按照权重来排序
    bool operator<(const Edge &w) const{
        return w<w.w;
    }
}edges[N];

int find(int x){
    if(p[x]!=x){
        x = find(p[x]);
    }
    return p[x];
}

int main(){
    scanf("%d%d",&m,&n);

    for(int i = 0;i<m;i++){
        int a,b,w;
        scanf("%d%d%d",&a,&b,&w);
        edges[i] = {a,b,w};
    }

    //kruskal
    sort(edges,edges+m);
    //初始化并查集
    for(int i = 1;i<=n;i++){
        p[i] = i;
    }
    //从小到大枚举所有边
    for(int i = 0;i<m;i++){
        int a = edges[i].a,b = edges[i].b,w = edges[i].w;

        a = find(a),b = find(b);
        if(a!=b){
            p[a] = b;
            res = res +w;
            cnt++;
        }
    }
    if(cnt<n-1) cout<<"不连通"<<endl;
    else cout<<res<<endl;
}