机器学习

讲义地址

1 什么是机器学习

1.1 机器学习的定义

Arthur Samuel:在没有明确编程(设置)的情况下，使计算机具有学习能力的研究领域。
Tom Mitchell：如果一个计算机程序可以通过经验E使得其在处理任务T时获得更好的效果(这个效果的好坏用性能度量P来衡量),即通过P测定在T上的表现因E而提高。
对于机器人跳棋程序来说，经验E就是程序与人下几万次跳棋，任务T就是玩跳棋，性能度量就是与新对手玩跳棋时赢的概率。
对于垃圾邮件拦截程序来说，经验E就是观察人对不同邮件的分类，任务T就是将邮件分类为垃圾邮件和非垃圾邮件，性能度量就是正确归类的邮件比例。

1.2 学习算法

1 监督学习(supervised learning),主要思想就是我们会教计算机做某件事情。
2 无监督学习(unsupervised learning)，主要思想是让计算机自己学习。
其他热词：强化学习(reinforcement)，推荐系统(recommender system)
要点：在应用学习算法的实际建议。如果我想要开发机器学习系统，如何让那些最佳实践操作指导我的决定，用什么方式建立自己的系统。

2 监督学习

2.1 回归问题

假设我要预测房价，我收集到了一些现有的房价数据。想要知道750平米的房子的价格是多少呢？学习算法能做的一件事情就是根据数据画一条直线，或者说用一条直线拟合数据(粉色直线)。然后可以估计出房子的价值约为150k。除了用一条直线拟合数据，可以用二次函数或二阶多项式(蓝色曲线)。然后可以估计出房子的价值约为200k。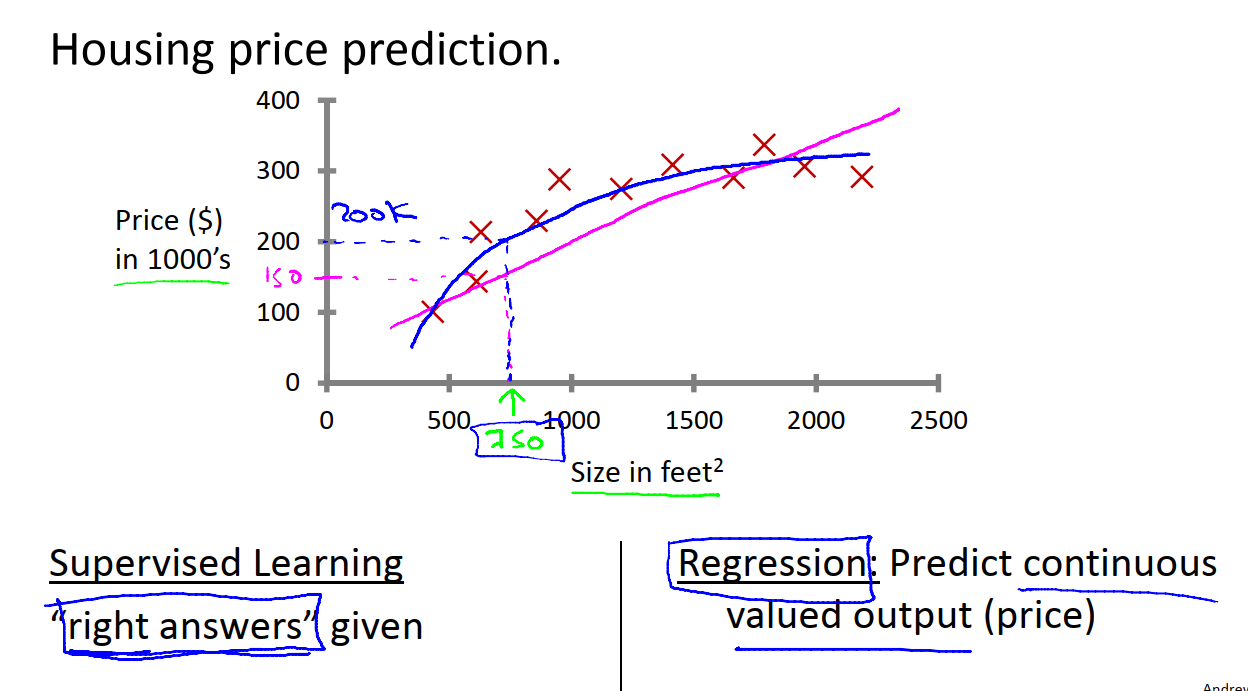

监督学习是指我们给算法一个数据集，其中包含了正确答案。也就是说我们给它一个房价数据集，在这个数据集中的每个样本，我们都给出正确的价格，即这个房子实际卖价。算法的目的就是给出更多的正确答案。例如得到面积为750的房子的价格。
用更专业的术语来定义，它也被称为回归问题。这里的回归问题指的是我们想要预测连续的数值输出，也就是房子的价格。在技术上来说，价格可以精确到分，因此实际上是一个离散值，但通常我们认为房价是一个实数，即连续值。回归这个术语是指我们设法预测连续值的属性。

2.2 分类问题

假设我想看医疗记录并设法预测乳腺癌是恶性的还是良性的。假设某人发现了一个乳腺肿瘤，即乳房上的肿块，恶性肿瘤就是有害且危险的，良性肿瘤就是无害的。
假设在我的数据集中，横轴是肿瘤的尺寸，纵轴表示我们看到的肿瘤样本是否是恶性的。然后有一个肿瘤样本的大小位于粉色箭头处，我们想要估计出肿瘤是良性还有恶性的概率。这就是一个分类问题。
分类问题就是我们设法预测一个离散值输出。对于这个问题，就是输出是0还是1。实际上在分类问题中，有时也可以有两个以上的可能的输出值。在实际例子中就是，可能有三种类型的乳腺癌，因此，可能的输出就有0(良性)，1(癌症类型1)，2(癌症类型2)和3(癌症类型3)。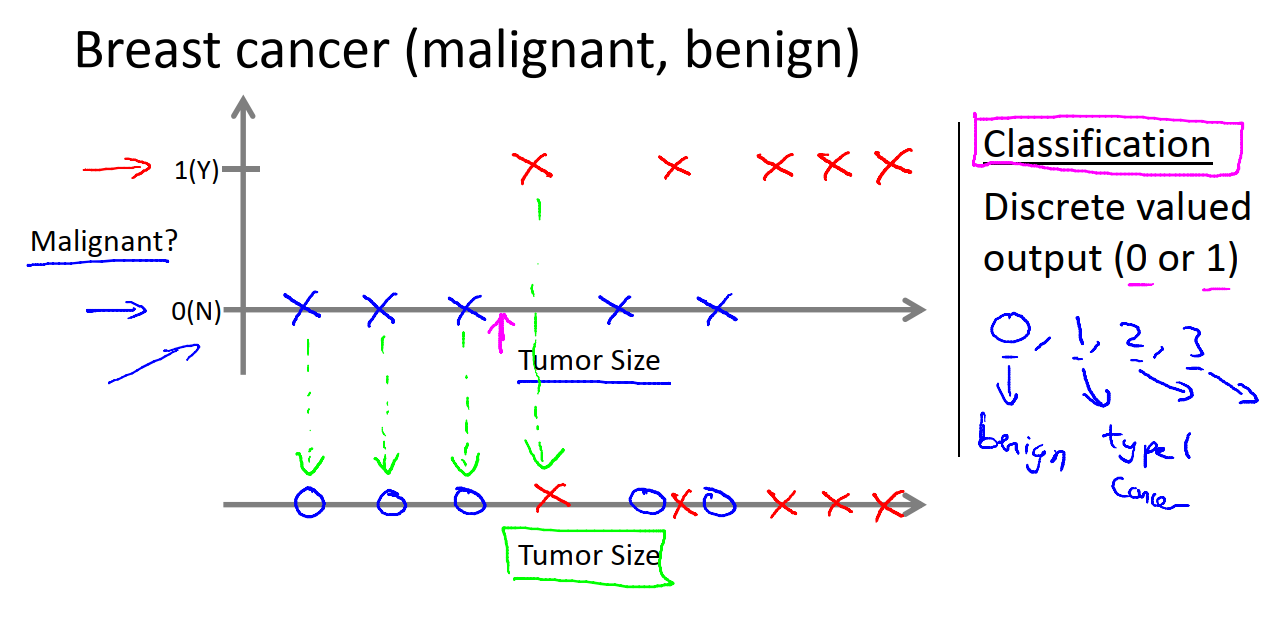

在分类问题中，有另一种方法来绘制这些数据。如果肿瘤的大小是预测恶性或良性的特征，我们可以在一个坐标轴上(表示肿瘤大小的坐标轴)，用不同的符号来表示良性或恶性(第二行的图)。在这个例子中，我们只使用了一个特征(属性)，即肿瘤得大小。在其他得机器学习问题中，我们会有多个特征(属性)。假设我们不仅知道肿瘤的大小，还知道病人的年纪，在这种情况下的数据集可以表示为下图。如果有一个患者，他的情况位于图中粉点处。因此在给定的数据集上，学习算法能做的，就是在数据上画出一条直线(黑色直线)，设法将恶性瘤和良性瘤分开，算法可以通过这条直线判断肿瘤的类型。在这个例子中，我们有两种特征，即病人的年龄和肿瘤大小。在其他的机器学习算法中，往往会有更多的特征，例如肿块的厚度，肿瘤细胞大小的均匀性，肿瘤细胞形状的均匀性。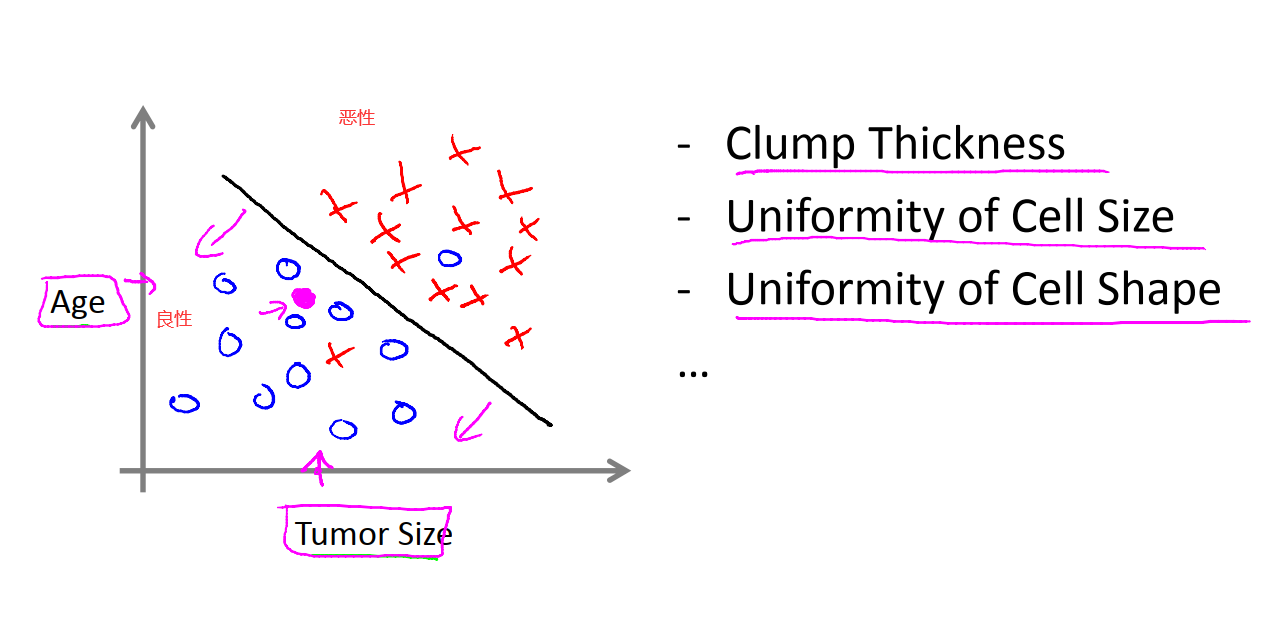

最有趣的机器学习算法，是一个不仅仅能处理两到三个或五个特征，而是能处理无穷多特征的算法，即如何在计算机中存储无穷维度的数据，而不会溢出呢？以支持向量机算法为例，就有一个灵活的数学技巧，允许计算机处理无穷多的特征。

2.3 总结

在这节课上我们讨论了监督学习，想法是在监督学习中，对于数据集中的每个样本，我们想要算法预测，并得出“正确答案”。像是房子的价格，或肿瘤是恶性还是良性的。
我们也讨论了回归问题，回归是指我们的目标是预测一个连续值输出。
我们还讨论了分类问题，其目的是预测离散值输出。

3 无监督学习

3.1 聚类

在上一节的监督学习中，我们的数据集中每个样本都被标明为阳性样本或阴性样本，即良性或恶性肿瘤。对于监督学习中的每个样本，我们已经被清楚地告知了什么是所谓的正确答案，即它们是良性还是恶性。在无监督学习中，我们所用的数据集中没有任何标签，我们试图在其中找到某种结构。无监督学习可能判定该数据集包含两个不同的簇。无监督学习算法，可以把这些数据分成两个不同的簇，这就是聚类算法。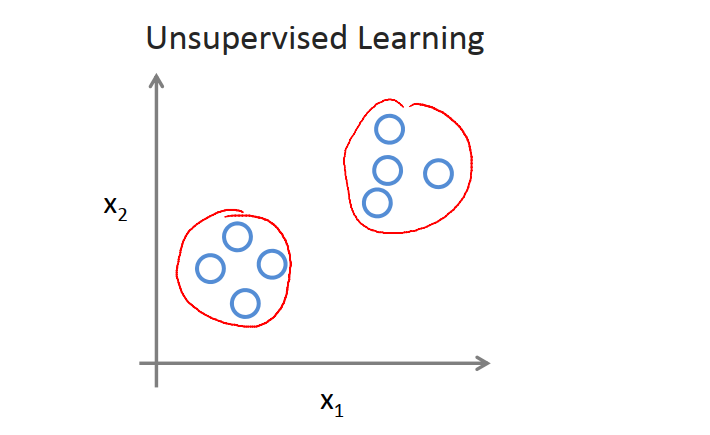

一个应用聚类算法的例子就是谷歌新闻。谷歌新闻所做的就是每天去网络上收集几十万条新闻，然后将它们组成一个个新闻专题。本质上就是将它们分簇，有关同一主题的新闻，被显示在一起。
其实聚类算法和无监督学习算法，也可以用于基因检测中。基因检测用于测定特定基因的表达程度，我们可以对测序结果进行聚类。
无监督学习或聚类算法可以用来组织大型的计算机集群。尝试找到那些机器趋向于协同工作，如果在实际使用中让这些机器共同工作，则数据中心可以更高效地工作。
聚类算法可以用于社交网络分析。如果可以得到我Email最频繁地联系人，机器就可以自动识别同属于一个圈子的朋友，判断哪些人互相认识。
聚类算法可以用于市场分析。许多公司利用庞大的客户信息数据库，对客户进行分类，从而能够自动高效地使用不同地策略进行销售。
聚类算法可以被用于天文数据分析，用于星系形成理论的研究。

3.2 鸡尾酒会算法

聚类算法只是无监督学习的一种。
鸡尾酒会问题。有一个宴会，有一屋子的人，大家都坐在一起说话，因为每个人都同时在说话，有许多声音混杂在一起，几乎很难听清楚面前的人说话。假设一个鸡尾酒会上只有两个人，也就是只有两个人在同时说话。我们放下了两个麦克风来记录来自两人声音的不同组合。两个人在两个麦克风的记录中声音大小不同，但是都是两个人话语重合的声音。
我们把这两个声音交给鸡尾酒会算法，让它帮忙找出数据的结构。鸡尾酒会算法会分离出这两个被叠加到一起的声音。或者是说话的声音和背景音。算法的主要代码为

[W,s,v] = svd((repmat(sum(x.*x,1),size(x,1),1).*x)*x');

在课程中使用的代码为Octave。svd函数全称为奇异值分解函数。

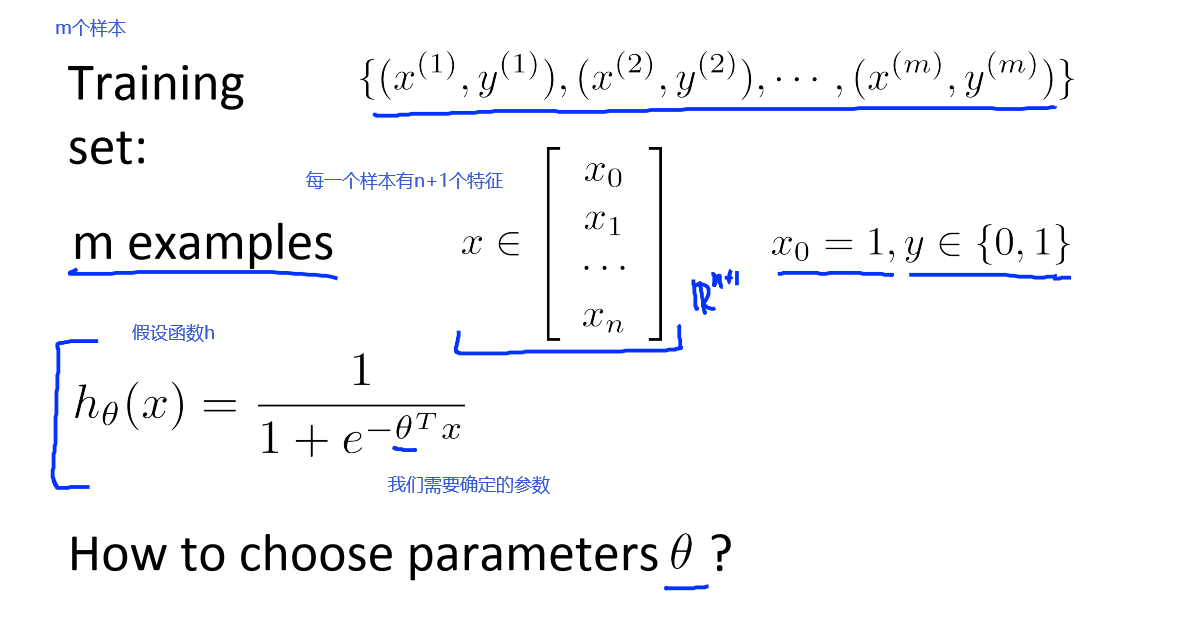
4 模型描述

回想2中预测房子价格的例子，根据已有的数据集，我们需要预测面积为1250的房子的价值。这是一个监督学习——对于数据集中的房子我们知道它们的面积和价格，这是一个回归问题——我们预测一个具体的数值输出。另一种常见的监督学习问题——分类问题，我们用它来预测离散值输出。
在建模过程中的符号如下：
m:表示训练样本的数量。
x’s:输入变量/特征。
y’s:输出变量/标签变量。
(x,y)表示一个训练样本。

$$(x^{(i)},y^{(i)})$$

表示第i个训练样本，上标i是训练集的一个索引。
在上图中h表示假设函数，它的作用是把房子的大小作为输入变量，输出为相应房子的预测y值。h是一个从x到y的映射。我们将h表示为

$$h_\theta(x)=\theta_0+\theta_1*x,缩写为 h(x)$$

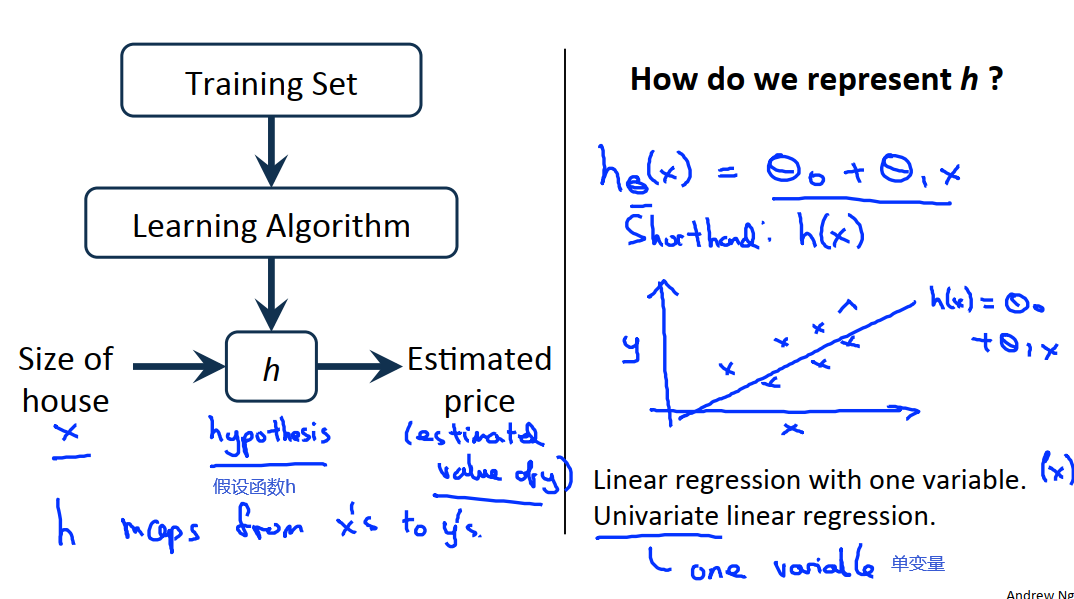
从表达式可以看出，y是一个关于x的线性函数(这是因为我们要从最基础的拟合开始讲起)。我们将从这个例子开始，先拟合线性函数，然后在此基础上，最终处理更加复杂的模型，以及学习更复杂的学习算法。这个模型被称为线性回归，这个例子为一元线性回归(单变量线性回归)。

5 代价函数

5.1 代价函数的定义

在这一节中，我们将定义代价函数的概念，帮助我们弄清楚如何把最有可能的直线与我们的数据相拟合。

$$h_\theta(x)=\theta_0+\theta_1*x,缩写为 h(x)$$ $$\theta_{i's}为模型参数$$

我们选择不同的θ值，就会得到不同的假设函数。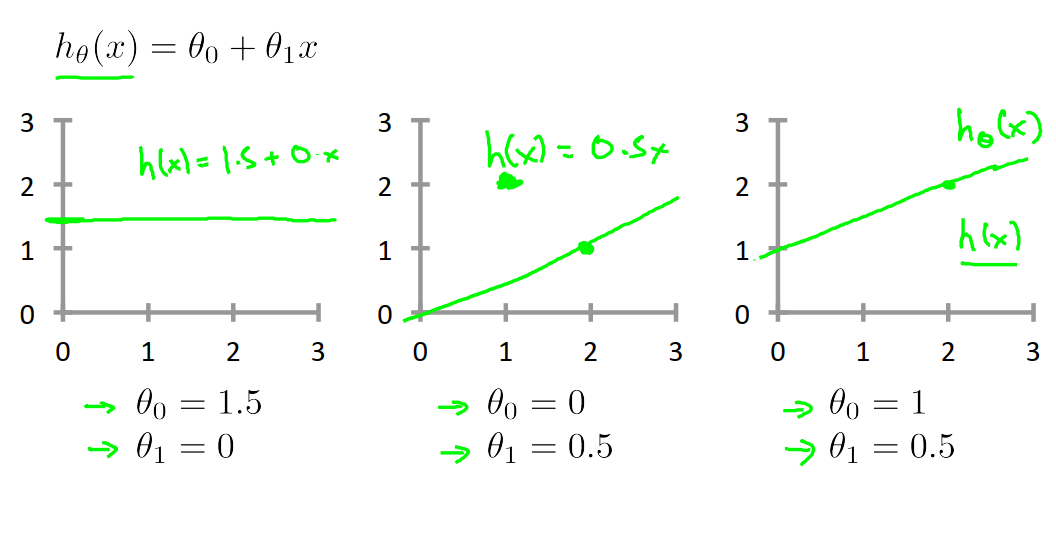

我们要做的就是得出θ0和θ1这两个参数的值，来让假设函数表示的直线尽量地与这些数据点很好的拟合。那么我们如何得出θ0和θ1的值来使它很好地拟合数据呢？我们要去选择能使h(x)也就是输入x时我们预测的值最接近该样本对应的y值的参数θ0和θ1。
在线性回归中，我们要解决的是一个最小化问题，使得下式的值最小。

$$minimize\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2$$

我们使用(x^(i),y^(i))表示第i个样本。m指的是训练集的样本容量。1/m 表示m个样本方差的均值，2是为了方便后面求导，其实是可以取任意实数，最终都会得出相同的θ0值和相同的θ1值，使得上式取得最小值。
我们将上述值定义成一个代价函数(cost function)如下：

$$J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2$$

其中，

$$h_\theta(x)=\theta_0+\theta_1*x$$

代价函数也被称作平方误差函数(Squard error function)，它可能是解决回归问题最常用的手段了。

5.2 代价函数的作用

实际上这包含了两个关键函数：
第一个是假设函数hθ(x),对于给定的θ，这是一个关于x的函数。
第二个是代价函数J(θ1)，是关于参数θ1的函数，它控制着h中直线的斜率。
当我们假设θ1=1时，我们求J(θ1)的值。

$$J(\theta_1)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2$$ $$J(\theta_1)=\frac{1}{2m}\sum_{i=1}^{m}(\theta_1x^{(i)}-y^{(i)})^2$$ $$J(\theta_1)=\frac{1}{2m}0^{2}+0^{2}+0^{2}=0^2$$

上述结果是在下图数据集的基础上得到的。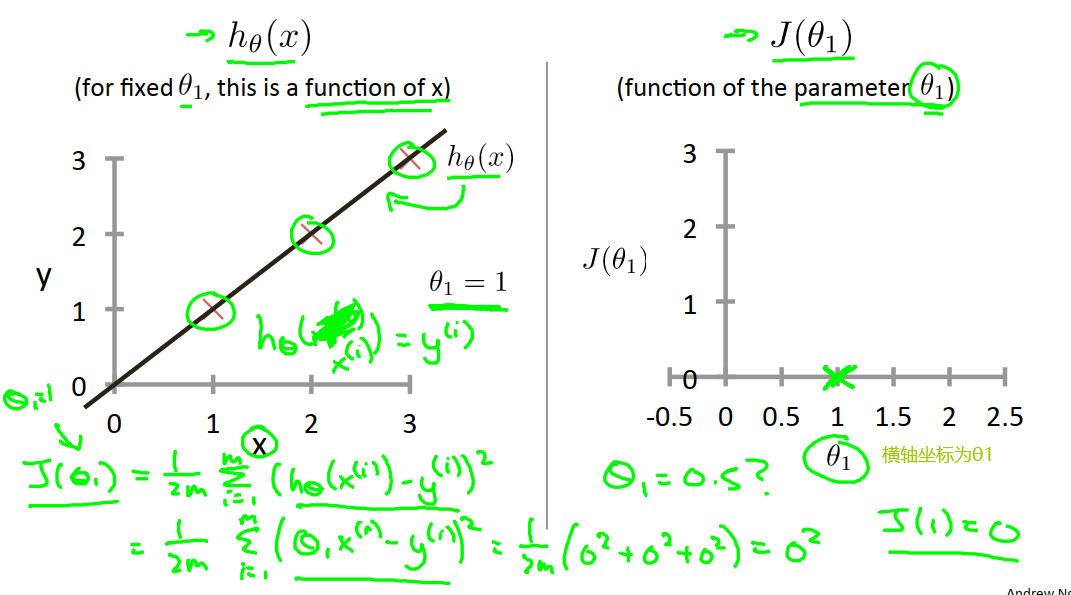

同理我们可以计算当θ1=0.5时，J(0.5)=7/12。当θ1=0时，J(0)=7/3。最终J(θ1)的函数图像如下：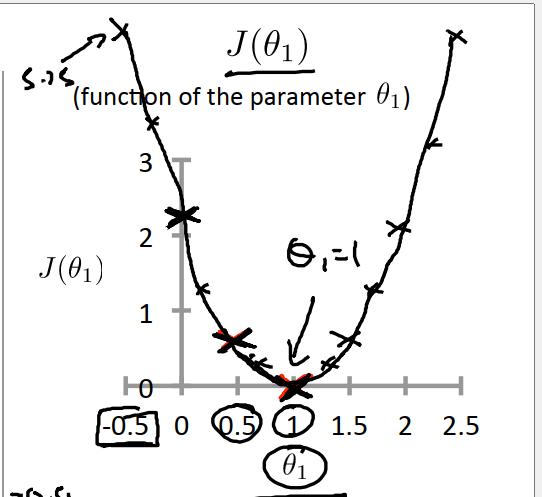

对于每个θ1，我们可以得到一个假设函数h，也可以得到损失函数J在θ1处的取值J(θ1)。优化算法的目标是我们通过选择不同的θ1，获得最小的J(θ1)，这就是线性回归的目标函数。在上图中，当θ1=1时，损失函数取得最小值。

5.3 代价函数的作用-plus

在上面的讨论中，为了简化问题，我们将θ0=0，现在我们保留全部参数θ0和θ1。则它的损失函数如下：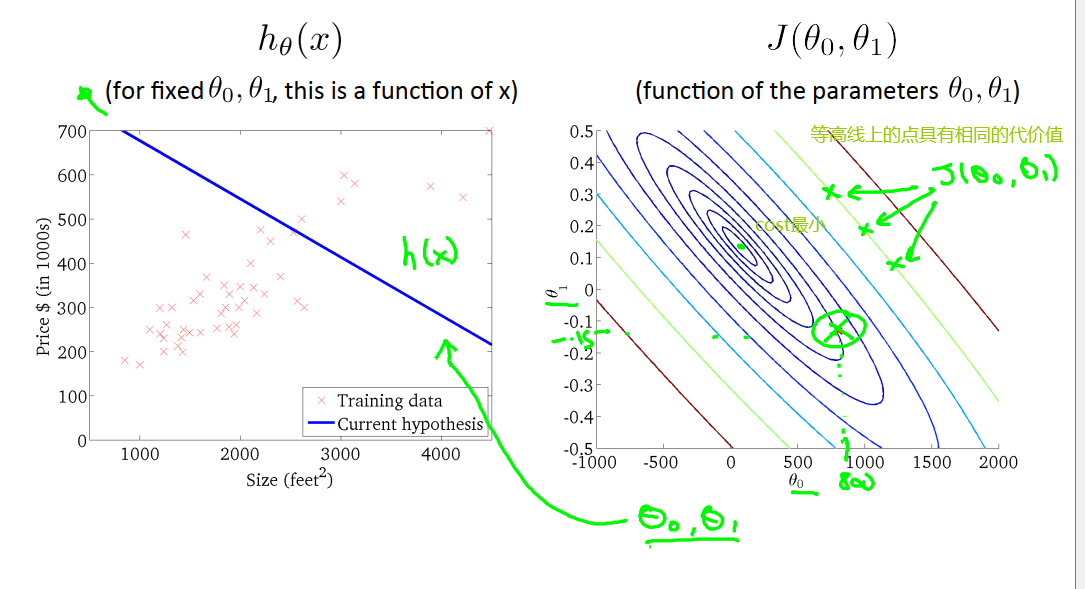

代价函数最小的点对应着更好的假设函数。

6 梯度下降

6.1 梯度下降算法步骤

梯度下降是很常用的算法，它不仅悲用在线性回归上，还被广泛用于机器学习的众多领域。我们可以使用梯度下降的方法去最小化线性回归的代价函数J，或是其他函数。
我们有一个函数J(θ0，θ1)，我们的目标是最小化J。
梯度下降的思路：
1)先给定θ0和θ1的初始值。初值到底是多少其实并不重要，但是一般将θ0设为0，θ1也设为0。
2)不停地一点点地改变θ0和θ1，来使得J变小。直到我们找到J的最小值，或者局部最小值。
梯度下降的一个有趣的地方在于，从不同的初始值出发，可能得到不同的局部最优解。
我们将会一直重复下面操作，直到收敛。

$$\theta_j:=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1)(for j=0 and j=1)$$

在上式中，:=表示赋值。在Pascal中，a=b表示我断言a和b相等。α被称为学习率，α用来控制梯度下降时，我们迈出多大的步子。如果α很大，梯度下降就很迅速，我们会用大步子下山(损失函数值)。如果α很小，那么我们会迈着很小的小碎步下山。
实现梯度下降算法的微妙之处是，对于上述更新方程，我们需要同时更新θ0和θ1。具体方法如下：

temp0 = theta_0-alpha*dtheta0J
temp1 = theta_1-alpha*dtheta1J

同步更新是更自然的实现方法。

6.2 梯度下降相关知识

6.2.1 更新函数解释

$$\theta_j:=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1)(for j=1 and j=1)$$

α控制我们以多大幅度更新这个参数θj。为了能更好地理解这个式子，我们假设想要最小化的函数只有一个参数的情形。假如我们有一个代价函数J，只有一个参数θ1(同5中简化情况)。
假设此时我们的损失函数J(θ1)如下图，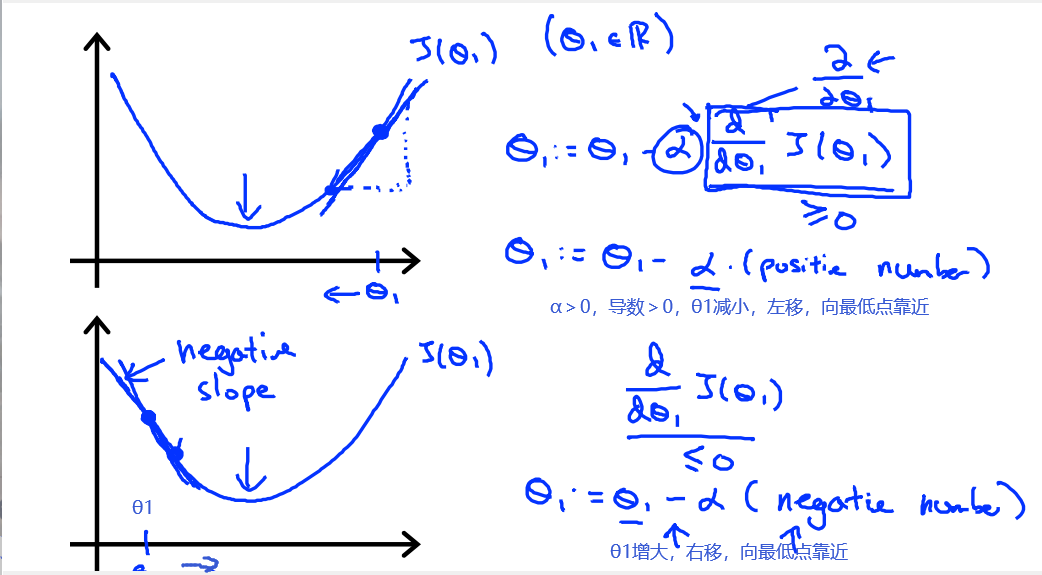

6.2.2 学习率解释

如果α过小(下图中上半部分情况)，就需要很多步才能到达最低点。
如果α过大(下图中下半部分情况)，那么梯度下降可能会越过最低点，甚至可能无法收敛。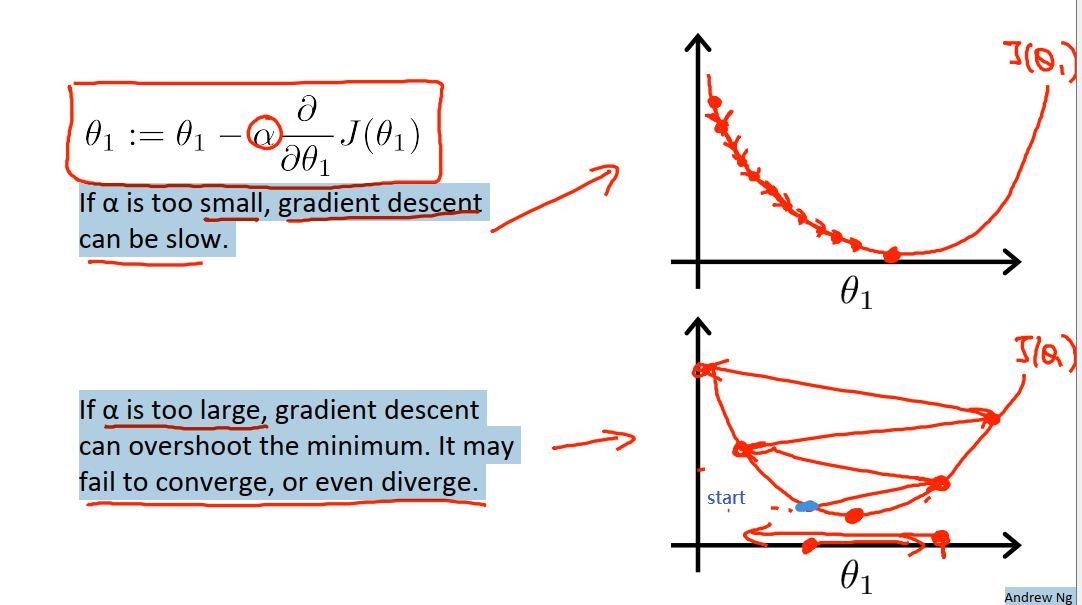

而如果θ1恰好初始化在局部最优点，那么梯度下降算法不会改变任何参数值。
梯度下降算法每次调整参数的大小不仅与规定的学习率α有关，也与当前θ点处的导数大小有关，越接近最低点，函数变化越平缓，导数越小，梯度下降算法调整参数的幅度就越小。所以实际上没有必要再另外减小α。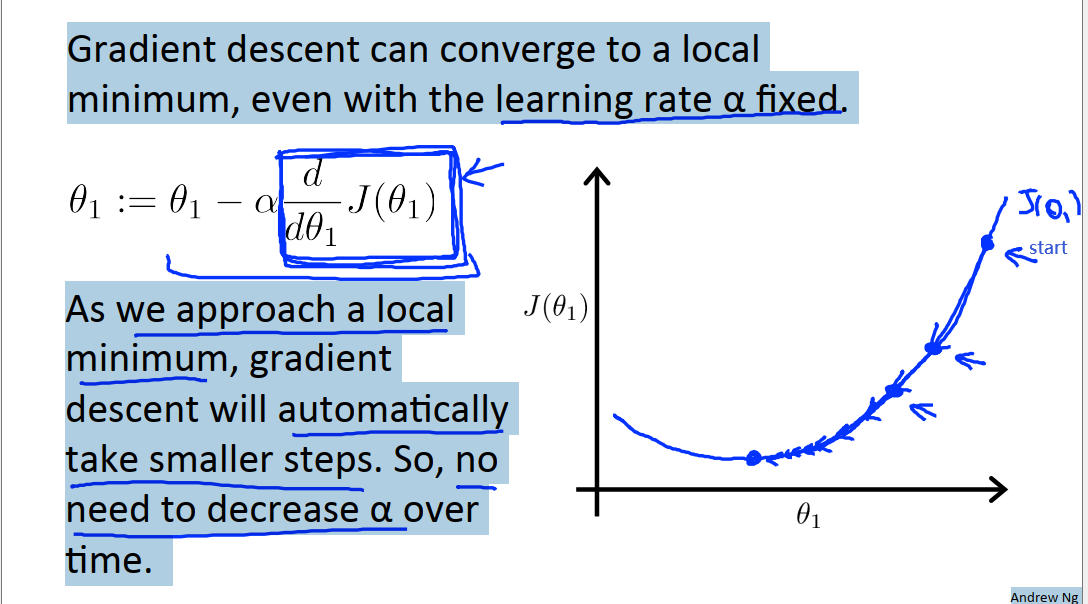

6.3 线性回归的梯度下降

本节中我们将梯度下降和线性回归中的代价函数结合，得到线性回归的算法。


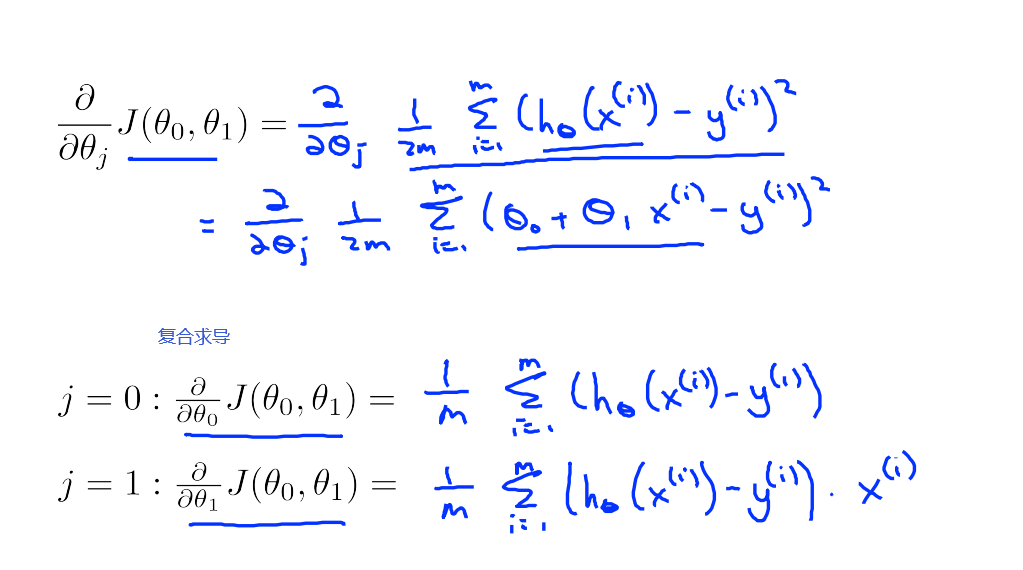
在求得偏导之后，我们带入上文中梯度下降的算法框架，得到

梯度下降容易陷入局部最优。但是线性回归的代价函数是一个碗状函数(二元)，术语叫凸函数，这个函数没有局部最优解，只有一个全局最优。当计算这种代价函数的梯度下降时，只要使用线性回归，它总会收敛到全局最优。
上文中我们讨论的梯度下降算法，被称为Batch梯度下降，Batch指的是每一步梯度下降，我们都遍历了整个训练集的样本。在梯度下降计算偏导数时，我们计算总和。还会有其他不是Batch模式的梯度下降算法，它没有全览整个训练集，每次只关注了小子集。
求解代价函数的最小值，我们还有最小二乘法(正规方程组解法)，但是相对于此方法，梯度下降法适合更大的数据集。

7 矩阵知识回顾

7.1 矩阵和向量定义

矩阵是指由数字组成的矩形数组。矩阵的维数：行数×列数。

$$R^{4\times 2}代表所有4\times 2的矩阵的集合$$

矩阵元素Aij表示矩阵中A中第i行第j列的元素。矩阵提供了一种很好的方式帮助我们快速整理、索引和访问大量数据。一般我们用大写字母表示矩阵，用小写字母表示数字/标量/向量。
一个向量时一种特殊的矩阵，向量是只有一列的矩阵，即维数为n×1，表示这是一个n维向量。R^4表示一个四维向量的集合。向量元素yi表示向量y的第i个元素。i可以从1开始(默认)，也可以从0开始。

7.2 矩阵运算

7.2.1 矩阵加法

只有相同维度的矩阵才可以相加。

7.2.2 矩阵标量运算

矩阵和标量的乘法运算。标量代表一个数字，或者实数。
3乘以矩阵A，等于将矩阵A中所有元素都逐一与3相乘。得到的结果是相同维度的矩阵。且乘法满足交换律。
矩阵A除以4，等同于0.25乘以矩阵A。

7.3.3 矩阵之间的乘法

矩阵相乘的前提是A矩阵的列数和B矩阵的行数相同。计算Aij的方法为让A的第i行元素分别乘以B中第j列的元素，并且相加起来。
我们可以利用矩阵乘法实现房价预测。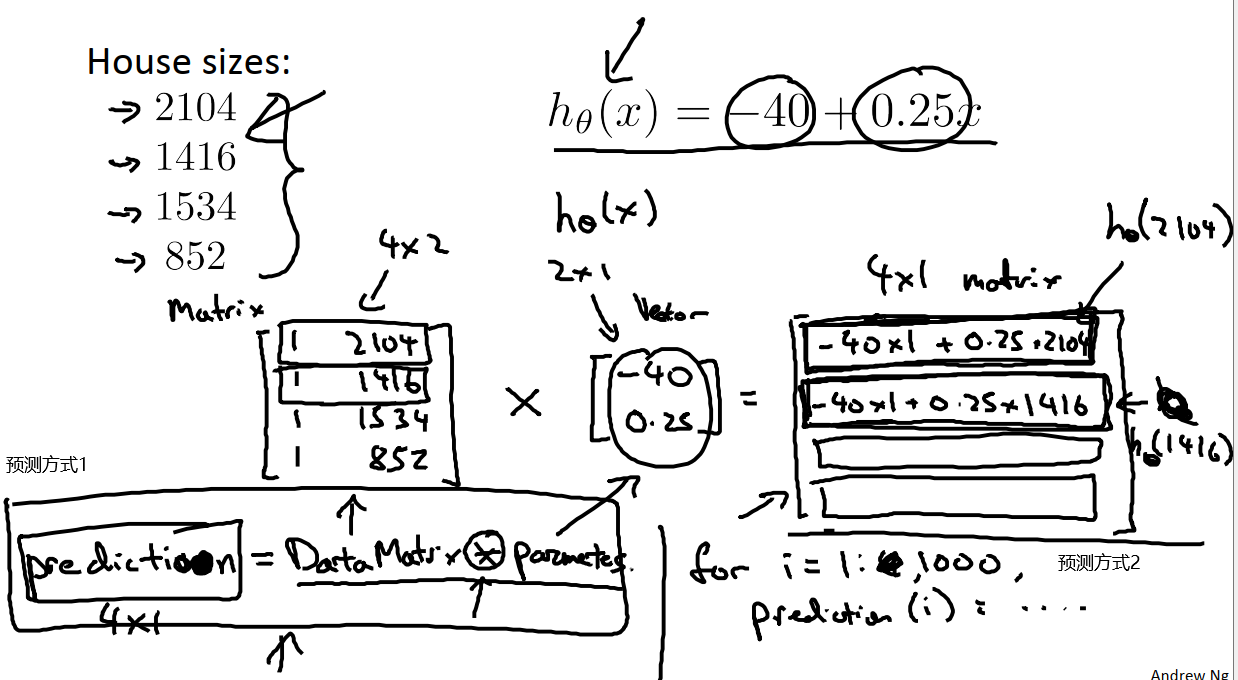

我们可以利用矩阵乘法实现更为细致的房价预测。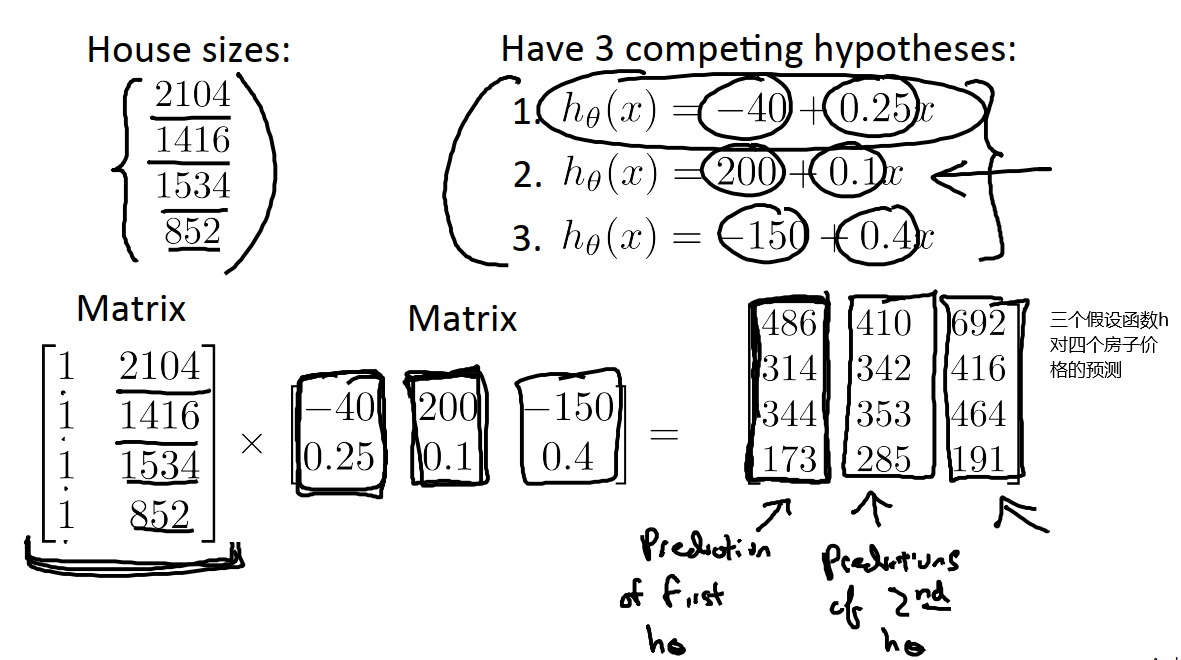

矩阵乘法的性质：
1)矩阵乘法不满足交换律。
2)矩阵乘法满足结合律。
3)幺元。在实数空间，1是一个乘法单位。在矩阵空间，单位矩阵是一个乘法单位，通常记作I(n×n)。对于A(m×n)矩阵来说，IA=AI=A，其中两个I的维度是不相同的，第一个是m×m，第二个是n×n。

7.3 逆和转置

7.3.1 矩阵的逆

在实数空间，每一个实数(除0外)都有一个倒数。在矩阵空间，如果矩阵A有逆矩阵A^(-1)，有

$$AA^{-1}=A^{-1}A=I$$

如果一个矩阵的行数和列数相同，那么称这个矩阵为方阵。只有满秩的方阵才有逆矩阵。我们把没有逆矩阵的矩阵称为“奇异矩阵”或是“退化矩阵”。python求解逆矩阵的代码为：

import numpy as np

a  = np.array([[1, 2], [3, 4]])  # 初始化一个非奇异矩阵(数组)
print(np.linalg.inv(a))  # 对应于MATLAB中 inv() 函数

# 矩阵对象可以通过 .I 更方便的求逆
A = np.matrix(a)
print(A.I)

7.3.2 矩阵的转置

A矩阵经过转置生成B矩阵，其特点是Aij=Bji。

8 多元线性回归

8.1 多元线性回归定义

在训练中我们会用到如下的符号：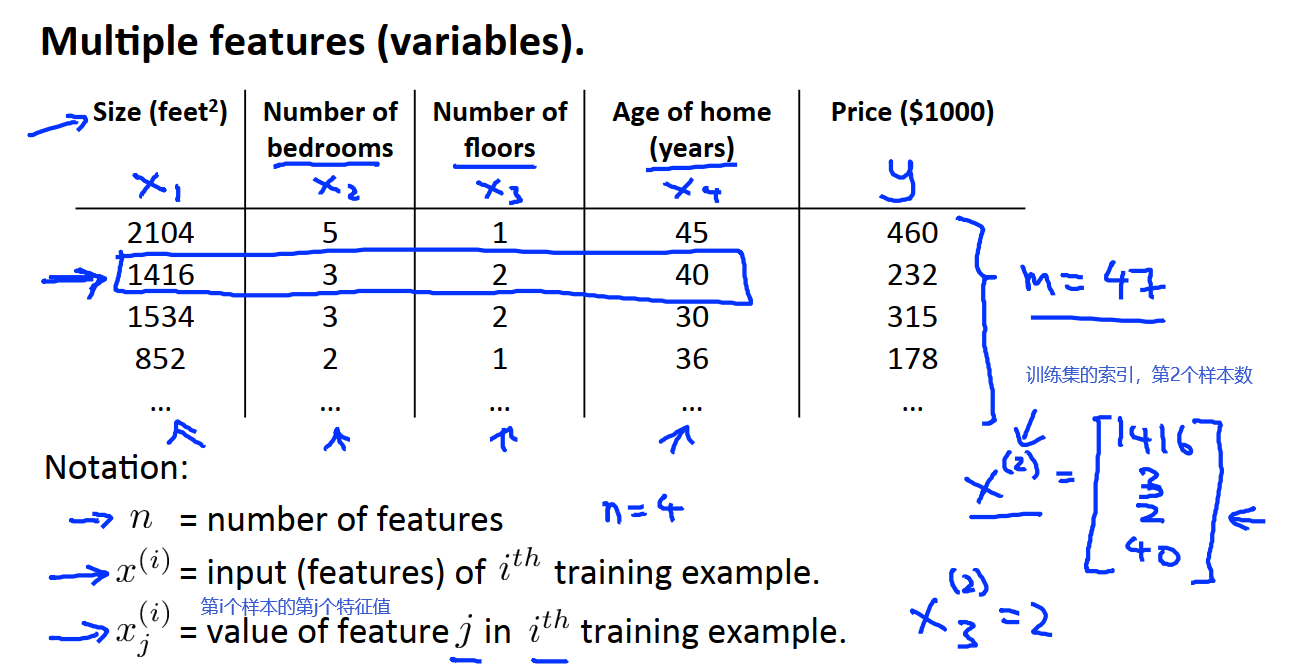

当我们有了多个特征量之后，我们的假设函数也需要相应变化。

$$h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_3+\theta_4x_4$$

然后我们引入矩阵乘法：

8.2 多元梯度下降法

8.2.1 多元梯度下降法的算法流程

通过上文的描述，我们可以把多元线性回归的模型参数看作是一个n+1维的向量θ。多元梯度下降法的算法流程如下：

8.2.2 多元梯度下降法——特征缩放

如果一个机器学习问题中有多个特征，且我能确保不同特征的取值都处在一个相近的范围内，这样梯度下降算法能更快地收敛。

使用特征缩放方法将特征的取值约束到-1到+1之间，也不一定是-1到+1，只需要不同特征的取值范围相近，梯度下降算法就可以正常地工作。
除了上图中将特征除以最大值的方法外，在特征缩放中，有时我们也会对特征进行均值归一化的工作。具体方法如下：

$$x_i = \frac{x_i-\mu_i}{max-min}$$

需要注意的是，我们不会对x0进行均值归一化的操作。上式的分母部分也可以是xi的标准差。

8.2.3 多元梯度下降法——学习率

为了保证梯度下降算法正确工作，我们可以绘制算法迭代次数-minJ(θ)的折线图，来展示梯度下降算法每次迭代之后，代价函数的值。如果算法正确运行，那么每一步迭代之后J(θ)都应该下降。当算法迭代到300-400次之间时，J(θ)的值已经下降的非常缓慢了。当算法迭代到400次时，从下图中可以看出已经差不多收敛了，因为代价函数值没有再继续下降了。

也可以采用自动收敛测试的办法：如果在一次迭代中J(θ)减小的幅度小于10^(-3)则认为算法收敛。但是想要寻找到一个合适的阈值是困难的。一般情况下我们可以通过上图中的折线图判断。
在使用梯度下降算法时，如果迭代次数-minJ的变化趋势如上图，则可以说明梯度下降算法在正常工作，反之，随着迭代次数的增加，J在不断上升或是波动，则证明梯度下降算法没有正常工作。此时，通常意味着算法应该使用较小的学习率α。
只要α足够小，那么每次迭代之后代价函数J都会下降。但是学习率不可以国小，那样的话梯度下降算法可能收敛得很慢。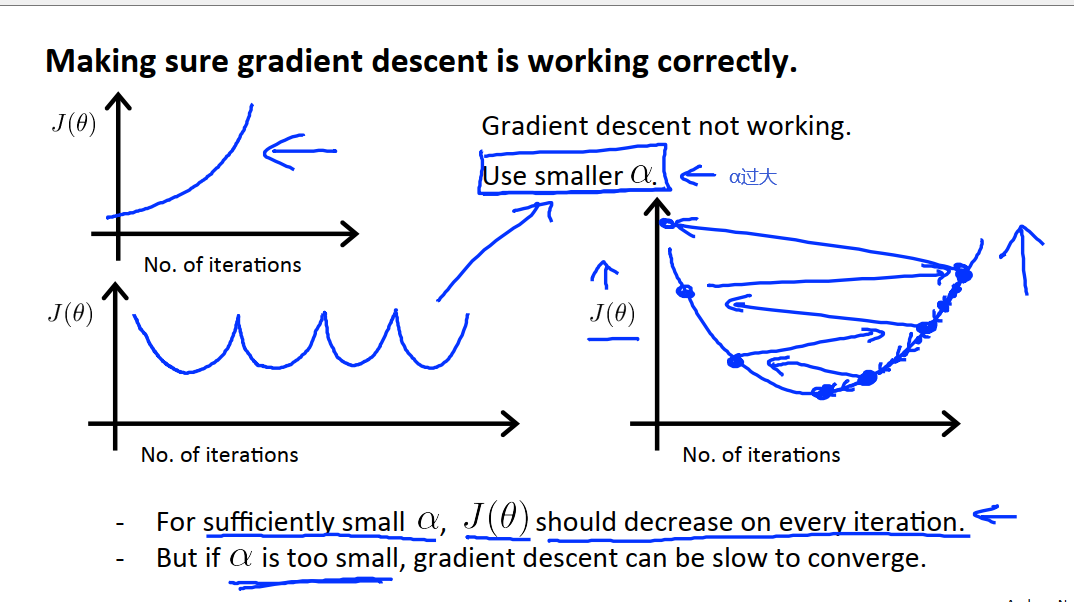

总结一下，如果学习率α太小的话，算法收敛速度会较慢；如果学习率α太大的话，代价函数J可能不会在每次迭代都下降，甚至可能不收敛。在一些情况下，如果α值太大，也可能会出现收敛缓慢的问题，但并不常见。为了了解算法的运行情况，通常需要绘制代价函数J随迭代步数变化的曲线。
尝试一系列α值，0.001，0.003，0.01，0.03，0.1，0.3，1……然后通过绘制J随迭代次数变化的曲线，选择一个使得J快速下降的α值。

9 特征和多项式回归

在房价预测中，我们可以将房子的长和宽两个特征合并为房子的面积这一个特征。这样就将特征从两个减少到一个。根据数据趋势，我们打算使用三次函数对特征进行拟合，如下图。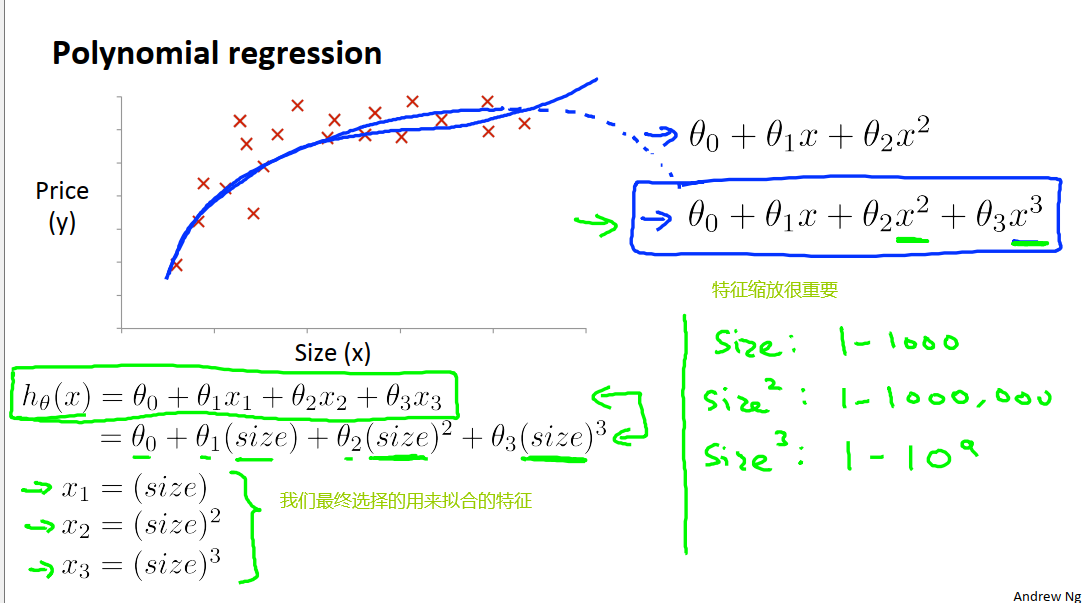

事实上，对于特征和假设函数，我们有更多的选择。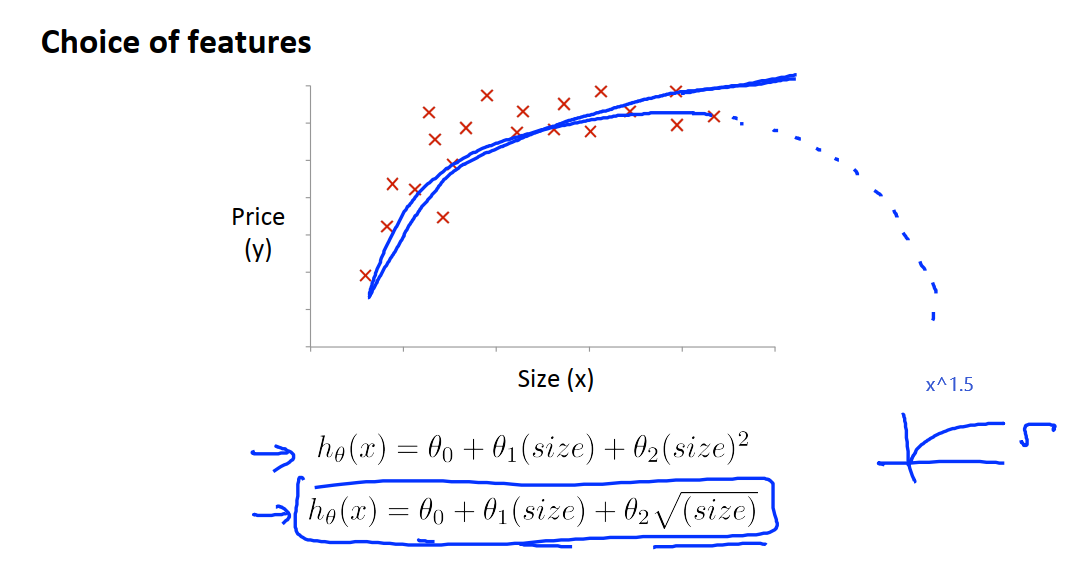

10 正规方程(区别于迭代方法的线性回归直接解法)

在上面我们了解了求minJ的梯度下降解法。正规方程提供了一种求θ的解析解法，使得我们不再需要运行迭代算法，而是可以直接一次性地求解θ的最优值。

10.1 正规方程求解流程

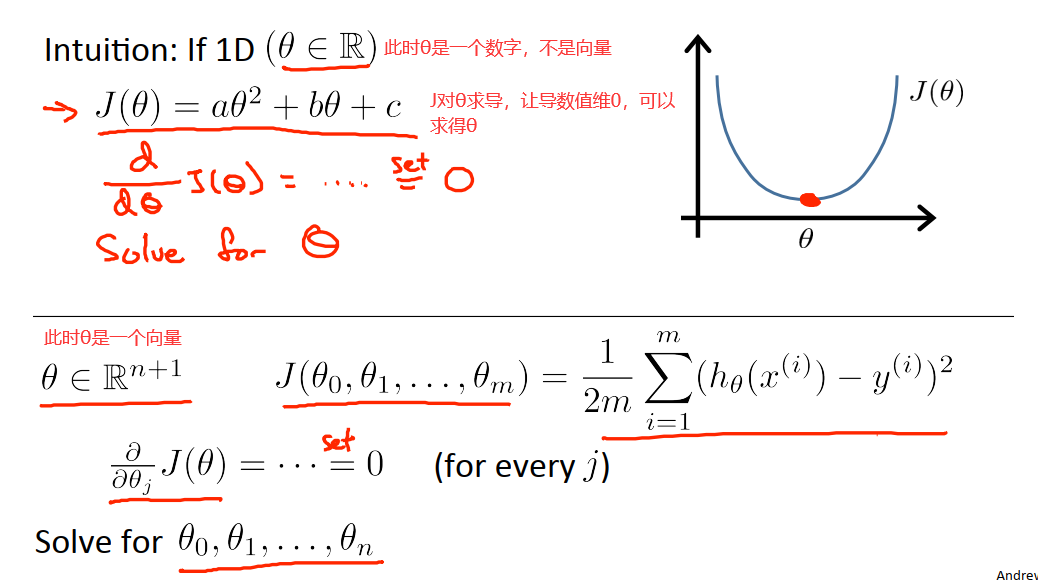
下面是具体计算过程。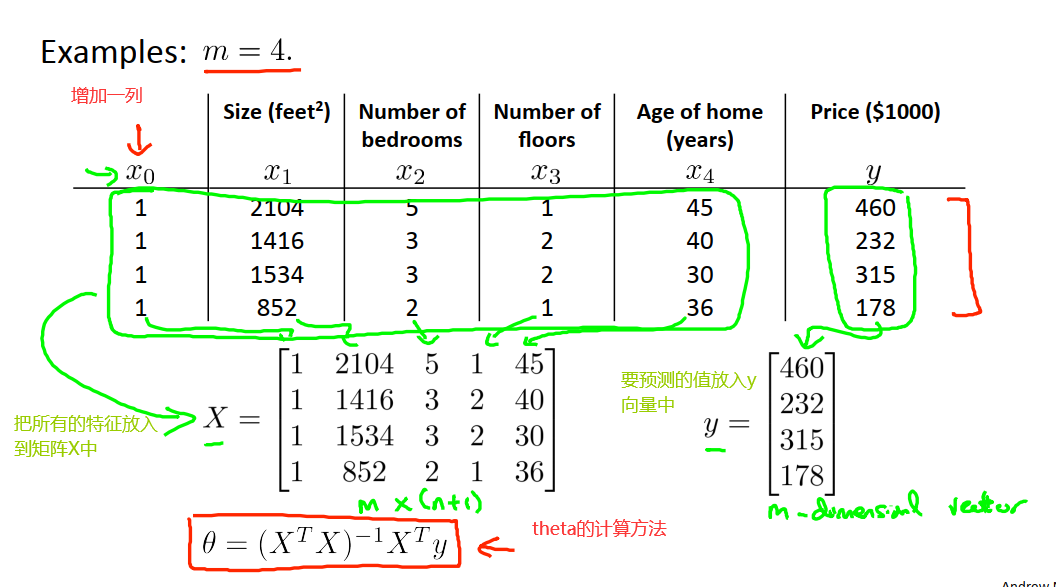

设计矩阵X的构造方法如下图。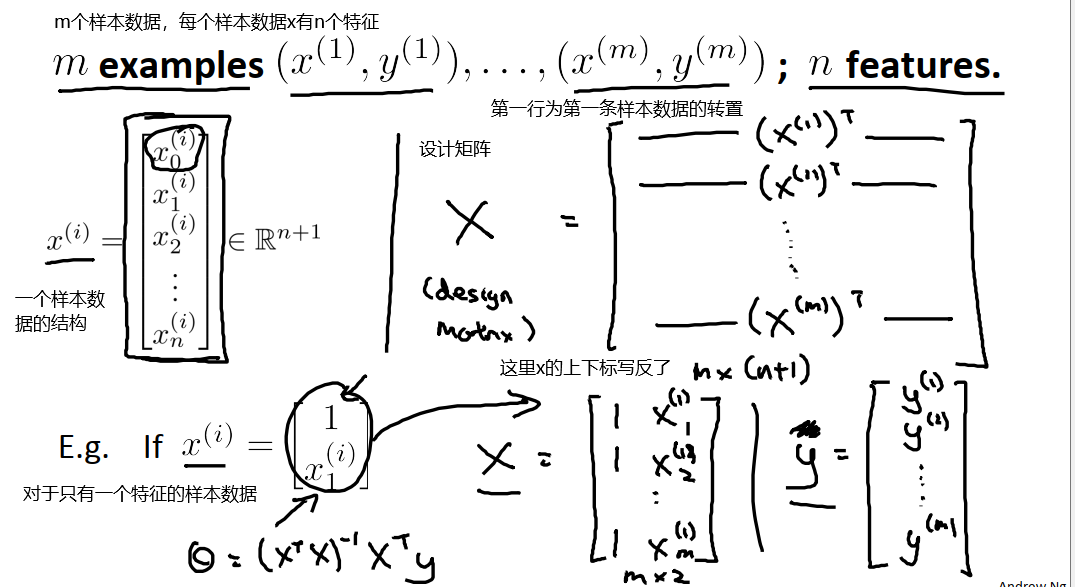

求解θ的关键是

$$\theta = (X^TX)^{-1}X^Ty$$

如果我们使用正规方程法求解θ，那么就不需要特征缩放。但特征缩放对于梯度下降法十分重要。
梯度下降法和标准方程法的适用范围：
梯度下降法(适用于特征较多，特征数为上万个)：
1 需要选择学习速率α。我们需要运行多次，尝试不同的α，找到运行效果最好的那个。
2 需要多次迭代。需要绘制迭代次数和损失函数J的曲线来检查收敛性。
3 在特征很多的情况下也能运行地相当好。
标准方程法(适用于特征较少，特征数为几千个)：
1 不需要选择学习速率α。
2 不需要迭代。
3 需要计算inv(X^T X),计算结果的维度为特征数(n+1)*(n+1),而逆矩阵的计算复杂度为O(n^3),当特征比较多时会比较慢。
当样本数据的特征数小于1万时，通常使用正规方程法进行线性回归，而不是用梯度下降法。

10.2 正规方程在矩阵不可逆情况下的解决方法

在上文中，我们通过下式计算θ。

$$\theta = (X^TX)^{-1}X^Ty$$

但是当XX^T不可逆时，也就是结果为奇异矩阵(或退化矩阵)时，正规方程解法可能会出现问题。在python中，我们可以通过计算矩阵的伪逆来解决这一问题。

import numpy as np

# 定义一个奇异阵 A 4×4
A = np.zeros((4, 4))
# 第一行，倒数第一个元素为1
A[0, -1] = 1
# 倒数第一行，第一个元素为-1
A[-1, 0] = -1
# 将A转化成矩阵
A = np.matrix(A)
print(A)
# print(A.I)  将报错，矩阵A为奇异矩阵，不可逆
print(np.linalg.pinv(A))   # 求矩阵A的伪逆（广义逆矩阵），对应于MATLAB中pinv()函数

XX^T矩阵不可逆的原因：
1 数据集中包含了多余的特征(线性相关的特征)。此时我们需要删除掉一部分线性相关的特征。如area和length，area= length*length，我们可以删掉area这个特征。
2 数据集中包含了太多的特征。例如数据集中一共只有4个样本，但是却有40个特征。此时我们需要删除掉一些特征，或使用正则化的方法。正则化方法可以帮助我们使用很多的特征来配置很多参数，即使我们有一个相对较小的训练集。

11 单变量线性回归实现

题目：假设你是一家餐厅的CEO，正在考虑开一家分店，根据该城市的人口数据预测其利润。
我们对梯度下降的算法进行向量化，可以得到每步更新的θ表达式为

$$\frac{\partial J}{\partial \theta}=\frac{1}{m}X^T(X\theta-Y)$$

具体推到过程如下：

11.1 读取文件

使用pandas读文件，得到一个类似于excel的表格。使用的函数为 pandas.read_csv()，关键参数如下：
1 filepath_or_buffer:字符串类型，要读取的文件存放路径，可以是http和文件
2 sep：字符串类型，分隔符，默认为’,’
3 header:整数，指定第几行作为列名(忽略注解行)，如果没有指定列名默认header=0,即文件中没有列名
4 names列表类型，指定列名
使用实例为：

# pandas是基于numpy的一种工具，该工具是为了解决数据分析任务而创建的
import pandas as pd
data = pd.read_csv(filepath_or_buffer='ex1data1.txt',names=['population','profit'])

11.2 数据集准备

绘制数据集的散点图，DataFrame使用data.plot.scatter()方法，关键参数如下：
1 横坐标
2 纵坐标
3 c：绘图使用的颜色
4 label:表示散点图的标签
5 s:表示绘制的散点的大小
使用实例为：

data.plot.scatter('population','profit',c='b',label='population',s=30)

根据上图中的推导，X矩阵的第一列全为1，所以我们需要在population前面插入一列1。使用的方法为DataFrame.insert(loc,column,value,allow_duplicates=False),关键参数为：
1 loc:插入的列索引，如要插入最前面，那么col=0
2 column:插入列的标签，字符串
3 value:插入列的值
使用实例:

data.insert(0,'ones',1)
# 注意没有赋值，不可以写成data=data.insert()的形式

在完成插入之后，我们需要将X矩阵的Y矩阵分离开。使用的方法为DataFrame.iloc(),使用的方法为：

X = data.iloc[:,0:-1]
# :表示所有的行都要参与切片
# 0:-1表示从第0列开始，到-1表示最后一列，但是取不到最后一列[0,-1)
Y = data.iloc[:,-1]
# -1表示将最后一列切片出来

因为后面我们需要涉及到矩阵运算，所以需要把DataFrame的类型变为数组型的，便于后续计算。DataFrame转换成ndarray的方法有：
1 df.values
2 df.as_matrix()
3 np.array(df)
使用实例：

X = X.values
Y = Y.values

接下来我们查看一下数据的维度：

X.shape

11.3 损失函数

因为X是2维数组(shape有两个值)，Y是1维数组(shape只有一个值)为了后续运算方便，我们把Y也改成2维数组。方法为:

Y = Y.reshape(97,1)

接下来，我们需要定义代价函数。我们的依据是：

$$J(\theta)=\frac{1}{2m}SUM(X\theta-y)^2$$

def costFunction(X,Y,theta):
    inner = np.power(X @ theta -Y,2) # @ 表示矩阵相乘
    return np.sum(inner)/(2*len(X))

然后，我们对θ进行初始化。θ的维度为2×1。

theta = np.zeros((2,1))

最后我们就可以计算出损失函数的初始值了。

cost_init = costFunction(X,Y,theta)

11.4 梯度下降函数

我们更新θ的依据为：

$$\frac{\partial J}{\partial \theta}=\frac{1}{m}X^T(X\theta-Y)$$

def gradientDescent(X,Y,theta,alpha,iters):
    costs = [] # 用于存储迭代过程中的cost
    for i in range(iters):
        theta = theta - (X.T @ (X @ theta - Y)) * alpha/len(X)
        cost = costFunction(X,Y,theta)
        costs.append(cost)
        # 打印一些cost
        if i%100 == 0:
            print(cost)
    return theta,costs

我们设置的学习率和迭代次数如下,然后调用函数开始迭代。

alpha = 0.02
iters = 2000
theta,costs = gradientDescent(X,Y,theta,alpha,iters)

11.5 可视化损失函数

# numpy是一个科学计算库，处理多维数组，进行数据分析
import numpy as np
# matplotlib是python的2D绘图库 matplotlib.pyplot提供一个类似matlab的绘图框架
import matplotlib.pyplot as plt
# 通过该代码生成一幅空的图，ax是一个绘图的实例,后续可以使用ax继续往该图上添加元素
fig,ax = plt.subplots()
# 如果是散点图，则为scatter
# 因为costs是list，所以我们需要把int型的iters变成list，方法为np.arrange()
ax.plot(np.arange(iters),costs,'b')
# 通过ax这个实例设置x和y轴的label
ax.set(xlabel='iters',ylabel='costs',title='cost vs iters')
plt.show()
# 更高级的subplots用法,绘制2*3个统计图
fig,ax = plt.subplots(2,3)
# 第1行第一个图对应的实例名
ax[0,0]

11.6 拟合函数可视化

x = np.linspace(Y.min(),Y.max(),100) # 生成100个点，范围取决于Y,这是因为Y和X的范围差不多
y_ = theta[0,0]+ theta[1,0]*x
fig,ax = plt.subplots()
ax.scatter(X[:,-1],Y,label='training data')
ax.plot(x,y_,'r',label='predict')
ax.legend() # 显示label
ax.set(xlabel='population',ylabel='profit')
plt.show()

11.7 多变量线性回归

因为不同特征取值范围相差巨大，所以首先我们需要对特征进行归一化。在实现中我们使用的是z-score normalization，量化后的特征服从标准正态分布：

$$z = \frac{x_i-\mu}{\delta}$$

def normalize_feature(data):
    return data-data.mean()/data.std()
    # mean为均值，std为标准差

多α的cost-iters函数绘制方法：

fig,ax = plt.subplots()
for alpha in alpha_list:
    _,costs = gradientDescent(X,Y,theta,alpha,iters)
    ax.plot(np.arange(iters),costs,label=alpha)
    ax.legend()
ax.set(xlabel='iters',ylabel='costs',title='cost vs iters')
plt.show()

11.8 正规方程解法

我们求解的依据是

$$\theta = (X^TX)^{-1}X^TY$$

numpy.linalg模块包含线性代数的函数。使用这个模块，可以计算逆矩阵(inv)、求特征值、解线性方程以及求解行列式等。

def normalEquation(X,Y):
    theta = np.linalg.inv(X.T@X)@X.T@Y
    return theta

12 向量化

12.1 Octave基本操作

length A返回A矩阵中维度较大的维度。
分号意味着换行 C=[A B]将A放在B矩阵左边，行成矩阵C，C=[A； B]，将矩阵B放在矩阵A下面，行成矩阵C。
＊表示矩阵乘，.＊表示矩阵对应元素乘。通常情况下.表示对矩阵中每个元素进行处理。
对矩阵使用max，得到的结果是每一列的最大值。从第一维度操作，也就是按列操作取最大值，返回一行数据。第二维度操作，也就是按行取最大值，返回一列数据。
A＜3将会返回A矩阵中每个元素带入这个表达式得到的布尔值。
plt.savefig(“D:\machine learning\myplot.png”,dpi=600) 保存图片

12 2 向量化操作

13 logistic回归-分类

13.1 logistic回归特点

我们的标签分为两种，我们用0来表示negative类(良性肿瘤，表示没有某样东西)，用1表示positive类(恶性肿瘤，表示具有某样东西)。
下图中，我们使用线性回归的思路对数据集拟合出了一个假设函数，并且根据实际情况给出了我们的判断依据。通过计算每个样本的h值，并将h值与0.5进行比较，我们可以得到预测的结果。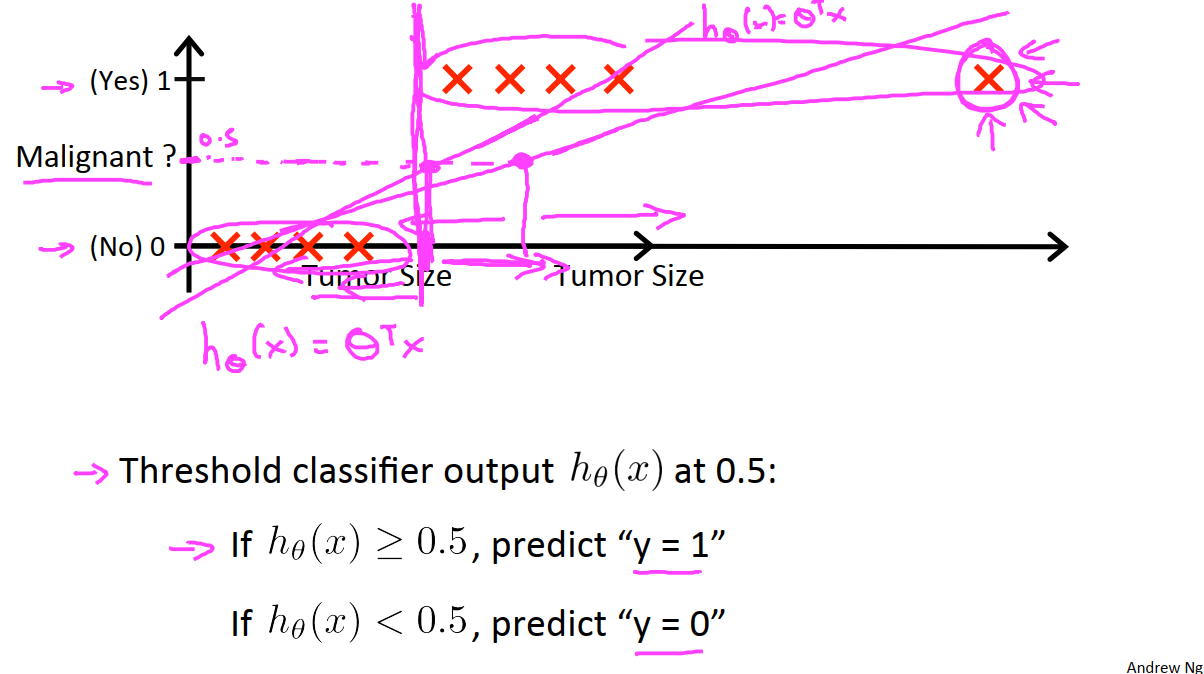

但是当我们新增一个样本点位于右上角时，就会给我们的假设函数带来比较大的改变，即使是这个样本点并没有任何新增的信息(使用原来的h函数可以很好地预测这个样本点的标签)。
因此把线性回归的思想应用于分类问题并不是一个好主意，所以我们有了logistic回归算法，它的特点是0≤h≤1。logistic回归算法属于一种分类算法。

13.2 假设陈述

在线性回归中，我们的假设函数h为：

$$h_\theta(x)=\theta^{T}x$$

对于逻辑回归，在此基础上修改，得到的假设函数h为：

$$h_\theta(x)=g(\theta^{T}x),其中g(z)=\frac{1}{1+e^{-z}}$$

g(z)称为sigmoid function(激活函数)或是logistic function(逻辑函数)。它的函数图像如下：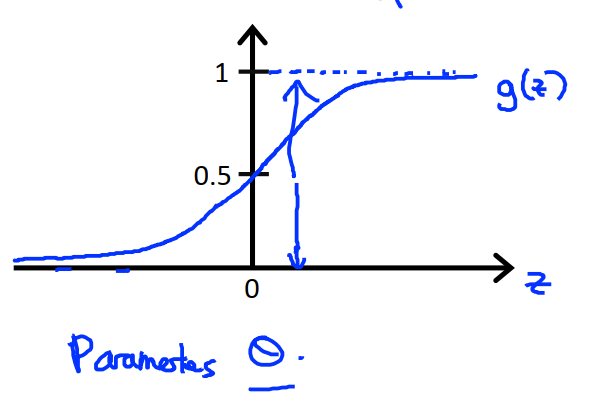

因此最终的假设函数为：

$$h_\theta(x)=\frac{1}{1+e^{-\theta^{T}x}}$$

假设函数h(x)的输出为：对于一个输入x，y=1的概率估计。

上图中，对于一个样本数据为x的患者，y=1的概率是0.7。这是一个后验概率。

13.3 决策界限

关于线性回归和逻辑回归的思考：
我们有一个二分类的样本，标签是0和1。首先根据样本做一个线性回归，得到一个假设函数h = θ^Tx,然后我们把这个假设函数h带入到激活函数中。激活函数输出的就是根据这个h函数的结果，这个标签y=1的概率是多少。阈值0.5，如果y=1的概率大于0.5，我们就预测这个输入的标签为1；小于0.5，就认为标签应该为0。所以激活函数的作用就是做一个概率评估，同时
添加非线性元素。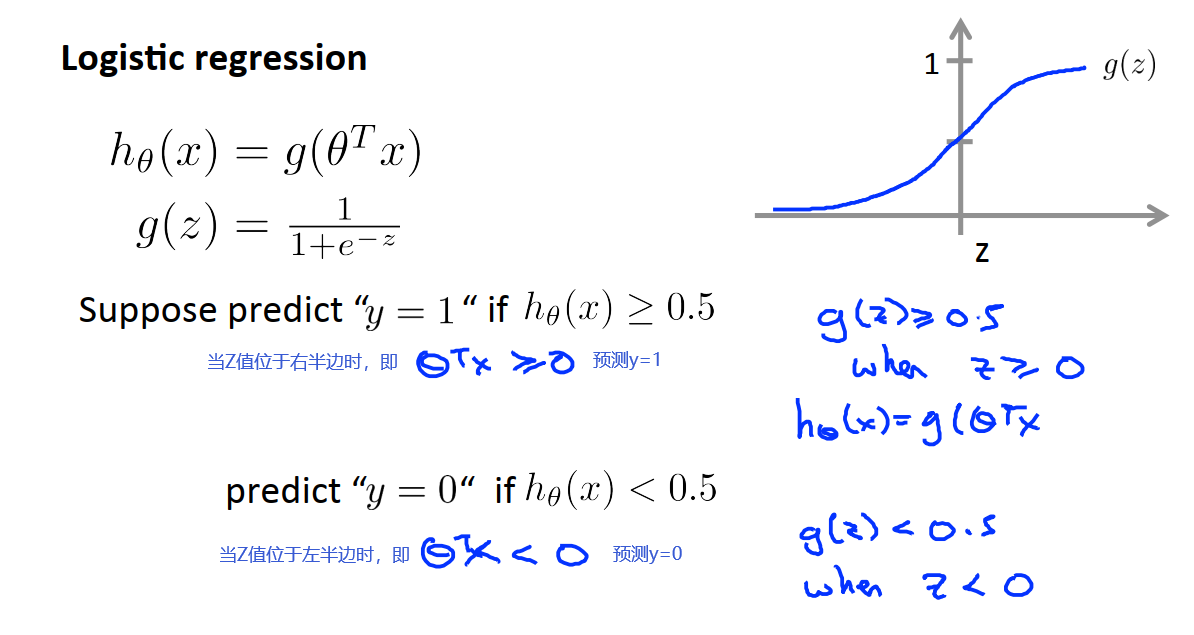

在下图中，我们列出参数向量θ，然后应用上图结论：当θ^Tx≥0时，预测y=1。得到了一个不等式，也就是我们在分类问题中使用到的决策平面。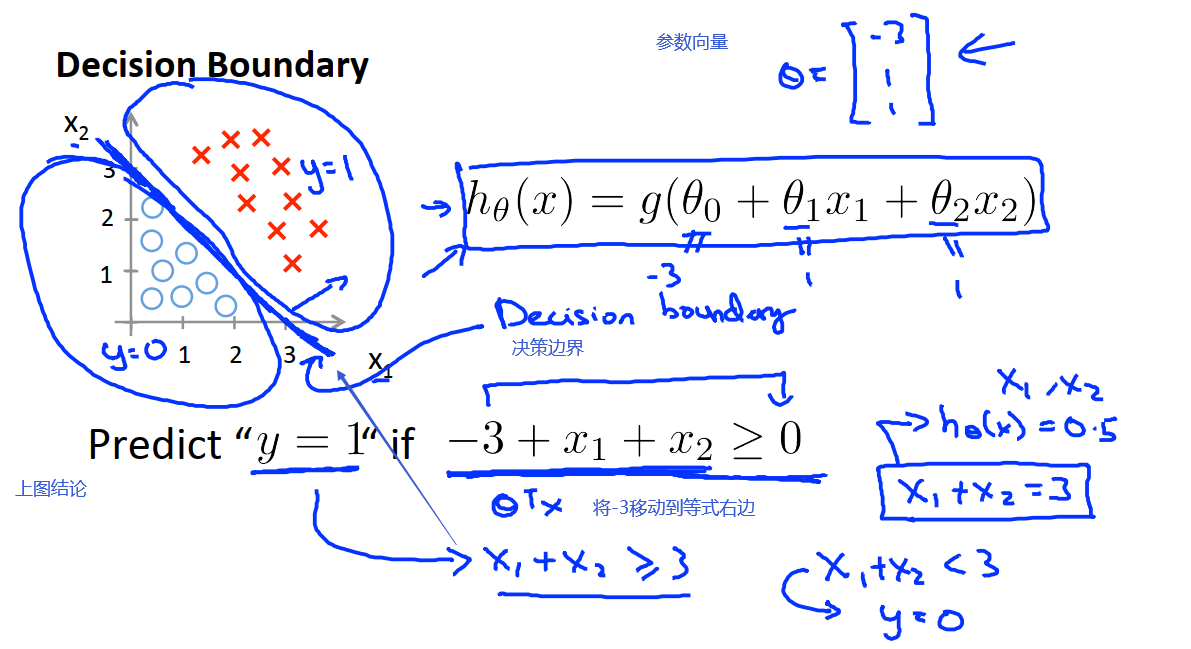

决策边界是假设函数h的一个属性，即使我们改变了数据集，这条决策边界以及我们预测y=1和y=0的区域，他们都是假设函数的属性，取决于其参数θ，而不是数据集的属性。我们使用数据集来确定参数theta的取值，但是一旦我们有确定的参数取值，我们就将完全确定决策边界。我们不是用训练集来定义的决策边界，我们是用训练集来拟合参数θ(我理解就是决策边界的形状其实是取决于我们确定的拟合函数，而不是训练集)。
如下图，我们可以在h中添加额外的高阶多项式项。假如我们已经通过下节中的方法得到了θ向量的取值。然后我们使得h≥0，得到决策平面是一个以原点为圆心的圆。

13.4 代价函数

在线性回归模型中，我们定义了代价函数J，在逻辑回归中，我们的代价函数为：

$$J(\theta)=\frac{1}{m}\sum_{i=1}^mCost(h_\theta(x^{(i)}),y^{(i)})$$ $$Cost(h_\theta(x^{(i)}),y^{(i)})=\frac{1}{2}(h_\theta(x^{(i)})-y^{(i)})^2$$

Cost函数的意义是在程序输出为h时，在实际标签为y的情况下，我们希望学习算法付出的代价。
但是如果我们按照这样的函数绘制出J-θ曲线，就会发现它是一个非凸函数，有很多局部最优值。如果我们对函数J使用梯度下降算法，不能保证他会收敛到全局最优值。我们希望代价函数是一个凸函数(单弓形函数)，只有一个局部最优值，这样我们可以保证梯度下降算法会收敛到该函数的全局最小值。
J(θ)函数之所以比较复杂的原因是因为在假设函数中引入了非线性的激活函数，且cost函数中还有平方操作，导致代价函数J有了很多个局部最优值。因此我们采用下图中的Cost函数带入到代价函数J中。

1：h(x)，即1/(1+e^f(z))值域为(0,1)，(0,1)同时作为cost(h(x),y)的定义域
2.以拟合y=1举例，Cost(h(x),y)取-log(h(x))
3.当h(x)=1时,-log(1) = 0，h(x)=0,-log(0)趋向于正无穷
4.-log(x)在(0,1)内单调递减，不存在局部最小值，合理的用梯度下降一定能收敛到全局最小值。
下图是y=0时的Cost函数。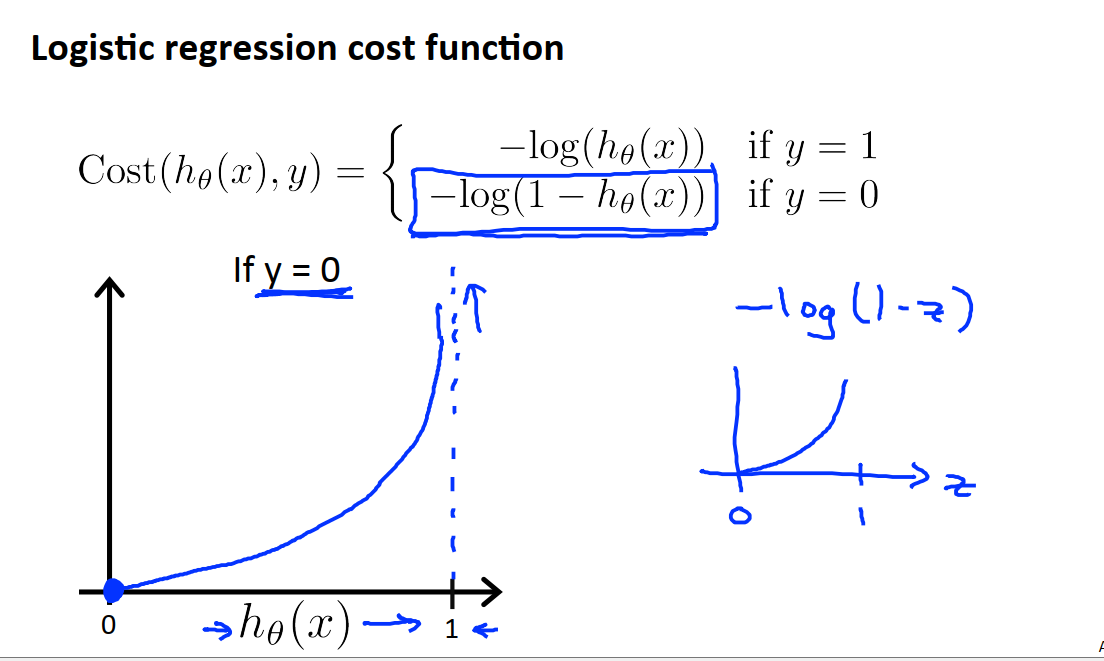

当y=1时，如果h=1，也就是说算法认为P(y=1)=1,那么Cost函数趋近于正无穷。

13.5 简化代价函数与梯度下降

我们定义的代价函数J如下：

$$J(\theta)=\frac{1}{m}\sum_{i=1}^mCost(h_\theta(x^{(i)}),y^{(i)})$$

简化后的Cost函数如下,它来自于统计学中的极大似然估计，在统计学中用于为不同的模型快速寻找参数，是一个局部最优值等于最值的函数。

$$Cost(h_\theta(x),y)=-ylog(h_\theta(x))-(1-y)(1-h_\theta(x))$$

接下来，我们的目标就是找出让损失函数J取得最小值的参数θ。我们使用梯度下降法。



为了观察梯度下降算法是否正常运行，我们同样可以绘制J-θ曲线。同时对于范围相差比较大的特征，我们也可以使用特征缩放的方法。

13.6 高级优化

给定θ，我们计算损失函数J(θ)和对θj的偏导数(for j = 0,1,…,n),然后带入到θj的更新函数中。如下图：

除了梯度下降法之外，我们还可以采用其他算法：
1 conjugate gradient(共轭梯度法)
2 BFGS
3 L-BFGS
这三种算法是在计算损失函数J(θ)和对θj的偏导数之后，使用比梯度下降法更复杂的算法来最小化代价函数。
他们的优点是：
1 不需要手动选择学习率α。我们可以认为他们有一个智能内循环(线搜索算法)，它可以尝试不同的学习速率并自动选择一个好的学习速率α。它甚至可以为每次迭代选择不同的学习速率。
2 收敛速度远远快于梯度下降。
缺点：比梯度下降法复杂。
在Octave中，我们可以使用内置的无约束最小化函数求解J(θ)的最小值。使用过程如下：

因此，对于logistic回归算法，我们也可以使用内置的无约束最小化函数求解，前提是我们需要定义一个costFunction，它可以返回此时的J(θ)和θ的梯度向量。

13.7 多元分类：一对多

接下来我们谈到的是如何使用logistic回归来解决多元分类问题。我们会介绍一个“一对多”的分类算法。
多元分类问题是指我们算法输出的标签不是0和1两种，可能会有三个标签或是四个标签等等。多分类问题的思想是“一对其他”，即将某一类从其他类别数据集中划分出来。具体思路如下图：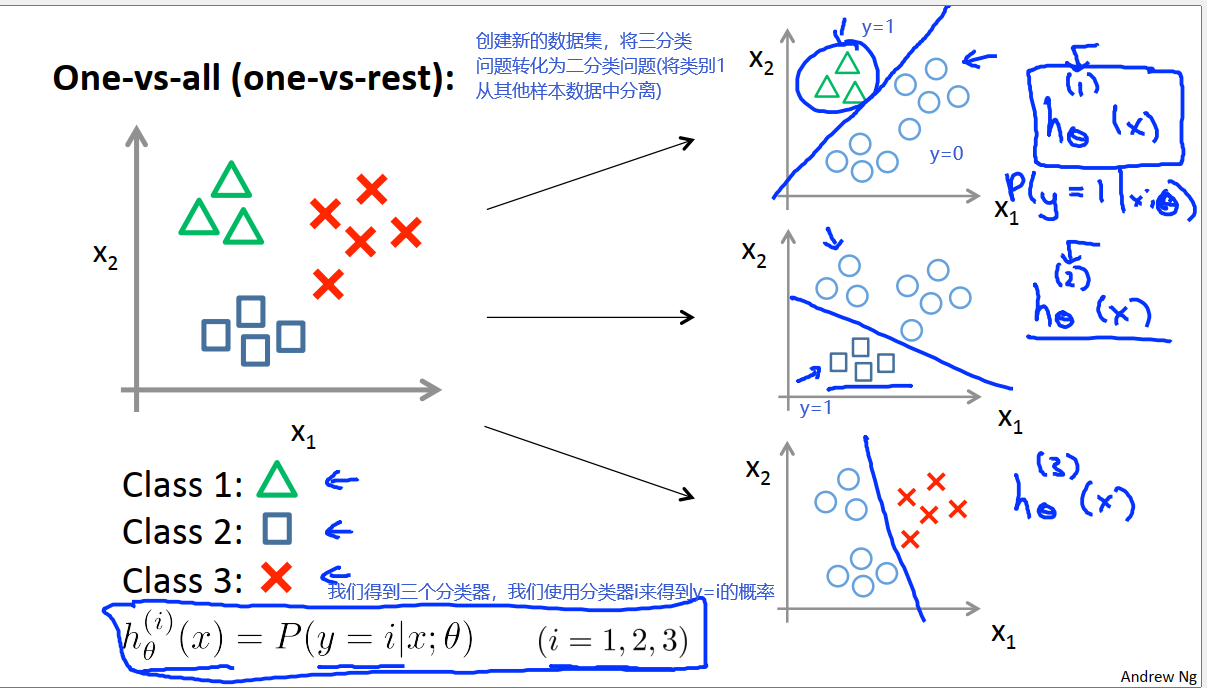

总之，对于类别i，我们训练一个逻辑回归分类器hi来预测y=i的概率。最终预测的结果是h最大的类别。

14 过拟合

14.1 什么是过拟合

14.1.1 线性回归中的拟合问题

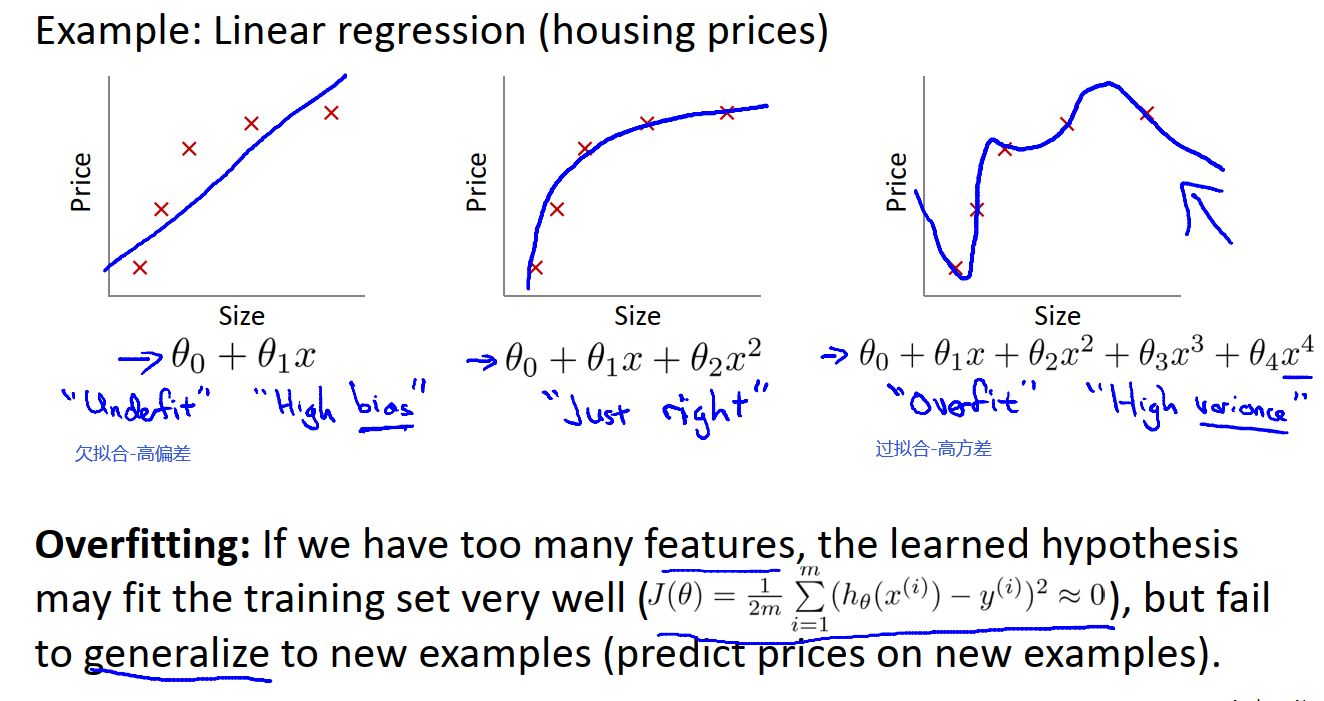
欠拟合-如果拟合一条直线，就好像算法有一个很强的偏见，或者说非常大的偏差，认为房子的价格与面积线性相关，而罔顾数据的不符，先入为主的拟合一条直线，最终导致拟合数据效果很差。
过拟合-拟合出来的曲线有很多的波动，即很高的方差。如果我们拟合一个高阶多项式，那么这个假设函数能拟合几乎所有的数据，这就可能面临假设函数太过庞大，变量太多的问题，我们没有足够的数据来约束它来获得一个很好的假设函数。
过拟合：如果我们有太多的特征，这时候训练得到的假设函数可以拟合训练集中的所有数据，但是它无法泛化(一个假设模型应用到新样本的能力)到新的样本中(没有出现在训练集中的样本)，那么就会有很高的方差(误差)。

14.1.2 逻辑回归中的拟合问题

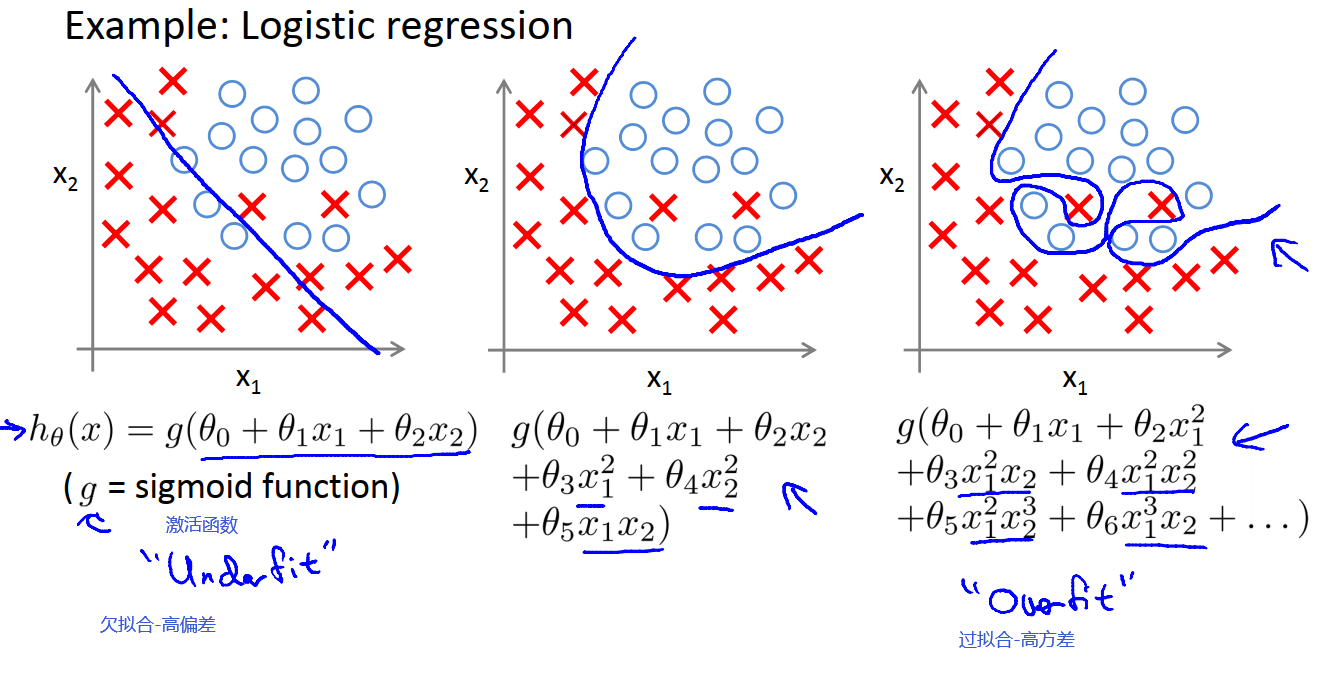
14.1.3 发现过拟合问题

在单变量线性回归中，我们可以通过绘制假设模型曲线，观察曲线的形状，可以作为决定多项式阶次的一种方法。在多变量线性回归中，如果我们有过多的变量，而且只有非常少的训练数据，就会出现过度拟合的问题。且多变量问题我们的画图等数据可视化工作会比较困难。

14.1.4 解决过拟合问题

我们有两个办法来解决过拟合问题：
一 尽量减少选取变量的数量。
1.1具体而言，我们可以人工检查变量清单，并以此决定哪些变量更为重要，哪些特征变量应该保留，哪些应该舍弃。
1.2模型选择算法(在后续课程中会讲到)。这种算法可以自动选择哪些特征变量保留，哪些舍弃。这种减少特侦变量的方法，可以有效减少过拟合的发生。但它的缺点是舍弃一部分特征变量，同时也舍弃了关于问题的一些信息。例如，也许所有的特征变量，对于预测房价都是有用的，我们实际上并不想舍弃这些信息或者这些特征变量。
二 正则化。
我们将保留所有的特征变量，但是减少量级，也就是参数θj的大小。这种方法非常有效，当我们有很多特征变量时，其中每一个变量都能对预测y值产生一点影响。

14.2 代价函数

下图中，我们在过拟合的函数中加入惩罚项，使得参数θ3和θ4都非常小。具体方法为在损失函数J中加入和θ3、θ4大小有关的项，当我们最小化代价函数后，θ3、θ4都会趋近于0，就像我们直接去掉了这两项一样，最后我们的拟合结果就会是一个二次函数加上一个非常小的项，也就是一个适当的拟合结果。这就是正则化背后的思想。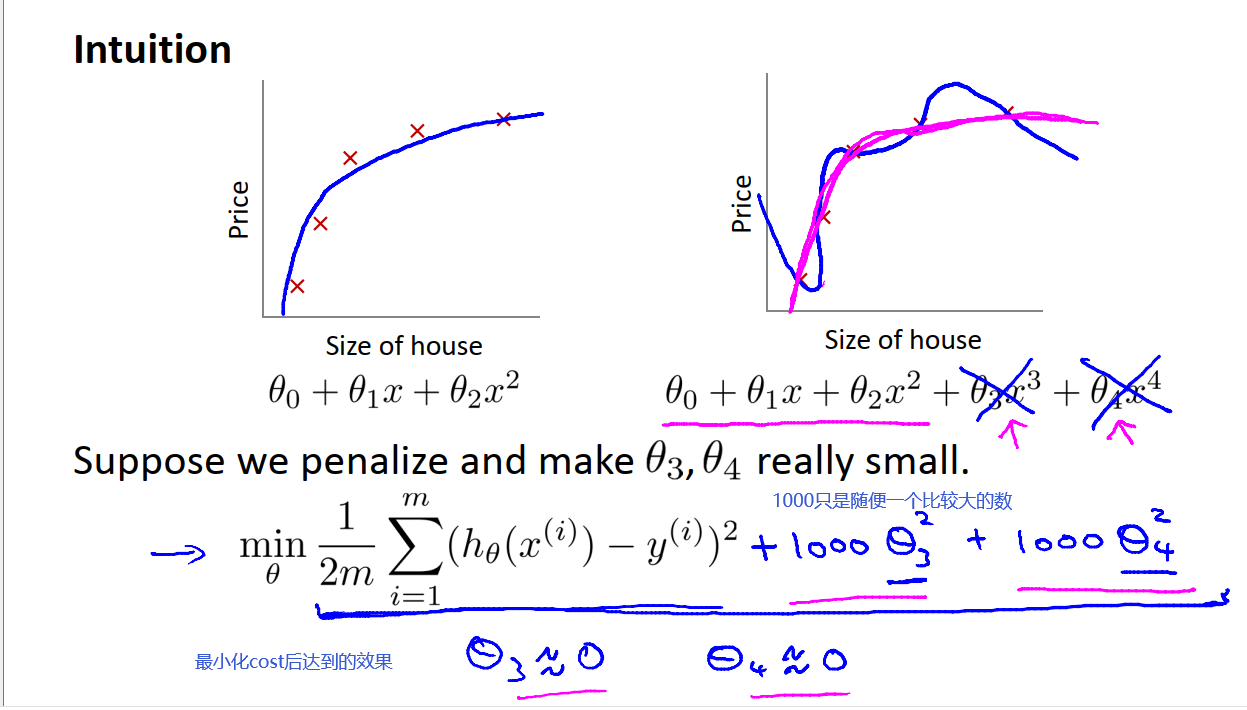

如果我们的参数值较小意味着：
1 一个更简单的假设函数(开头的例子)
2 如果参数的数值越小，我们得到的函数就会越平滑，也越简单。因此，也更不容易出现过拟合的问题。
例如我们在房价预测的过程中，可能有100个特征，我们就会有101个参数(多一个是因为我们加了一列全为1的特征)，但我们并不知道哪一个是高阶项，这使得我们很难预先挑选出其中的哪些参数来缩小它们的值。因此在正则化中，我们要做的就是修改线性回归的代价函数来缩小所有的参数(因为我们并不知道该选哪些参数去缩小)，我们将代价函数修改为下式，其中m是样本数，n是特征值个数，λ是正则化参数，控制两个不同目标之间的取舍(平衡关系)。我们的第一个目标就是想去训练一个假设函数能更好地拟合训练集(与损失函数的第一项有关)，第二个目标就是我们要保持参数尽量地小(与损失函数的第二项有关，与正则化目标有关)

$$J(\theta)=\frac{1}{2m}[\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum_{j=1}^{n}\theta_j^2]$$

我们在代价函数中增加一个额外的正则化项来缩小每个参数的值。我们可以注意到θ是从θ1开始计算的，所以我们并没有给θ0增加惩罚项，这是约定俗成的。
我们使用正则化代价函数之后，假设函数的变化如下图：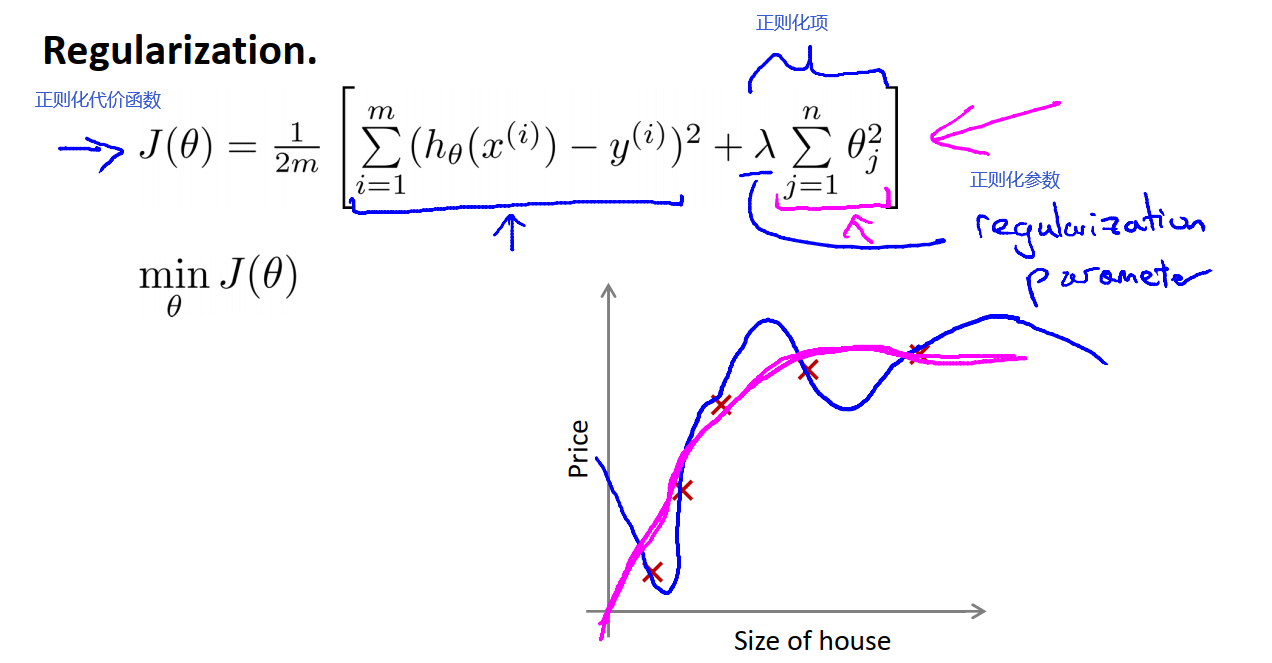

在正则化的线性回归中，如果正则化参数λ被设得太大的话，其结果就是我们对这些θ参数的惩罚程度过大，那么最后，这些参数都会接近于零，这样的话，就相当于把假设函数的全部项都忽略掉了，最后假设模型只剩一个θ0。于是我们最终的假设函数为h=θ0。这样就相当于我们直接用一条直线
去拟合数据，就会导致数据欠拟合。也就是这个假设模型的偏见性太强，与数据本身的趋势不符合，也与实际情况不符合。
为了让正则化起到应有的作用，我们应该去选择一个更合适的正则化参数λ。

14.3 线性回归的正则化

14.3.1 使用正则化的梯度下降解法

我们之前推导了两种求解线性回归的方法，一种基于梯度下降，一种基于正规方程。在本节，我们将这两种方法推广到正则化线性回归中去。在上文中，我们得到了正则化代价函数，如下式：

$$J(\theta)=\frac{1}{2m}[\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum_{j=1}^{n}\theta_j^2]$$

在没有加入正则化参数时，梯度下降算法更新θ的方式如下图：

在上图中，我们先单独更新了θ0，然后再更新了θj(j=1,n),这样做的目的是因为我们正则化线性回归的惩罚对象是参数θ1到θn，我们没有惩罚θ0，因此我们需要区别对待θ0。然后我们将θj的更新方式修改为图中最下面的式子。即加上了-αλθ_j/m，也就是在偏导数部分加上了λθ_j/m(Σθj^2/m对θj求偏导)，这实际上就是正则化代价函数J(θ)对θj的偏导数。
我们可以注意到，θj的系数(1-αλ/m)是一个只比1略小一点的数。这是因为通常学习率α很小，但m却很大，那么通常αλ/m会很小，所以(1-αλ/m)是一个只比1略小一点的数。所以θ更新的结果就是θj变成了θj*0.99，也就是把θj向0的方向缩小了一点点，这使得θj变小了一点点。然后θj更新中的第二项完全与我们在添加正则化项之前的梯度下降更新一样。
当我们在使用正则化线性回归时，我们要做的就是每次迭代时，都将θj乘以一个比1略小的数，我们每次都把参数缩小一点，然后进行和之前一样的更新操作。从数学角度来说，我们做的依然是对代价函数J(θ)使用梯度下降算法

14.3.2 使用正则化的正规方程解法

我们建立一个设计矩阵X，它的每一行都代表一个单独的训练样本。正规方程求解θ的关键是

$$\theta = (X^TX)^{-1}X^Ty$$

现在我们在使用正规化的正规方程解法来得到我们想要的最小值。求解θ的式子如下图：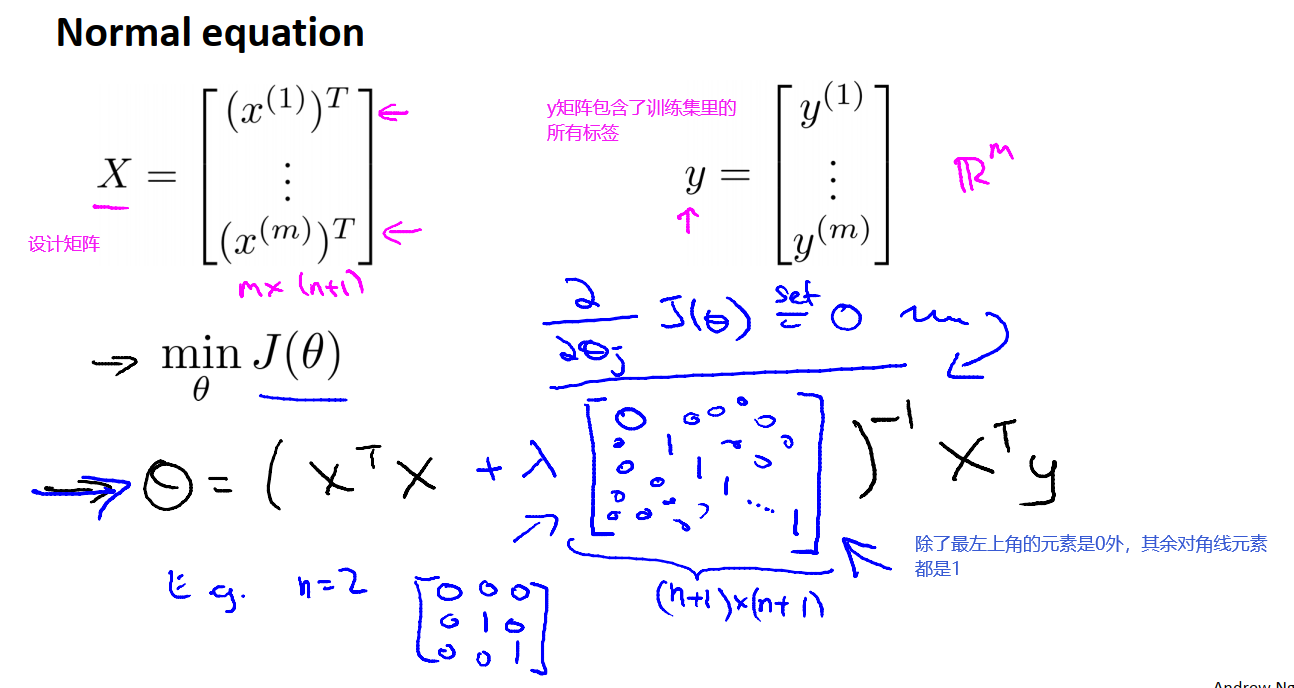

在求解θ过程中可能会遇到不可逆的问题。如果我们的样本总数m≤样本的特征向量n，那么X^TX就是不可逆的，或者是一个奇异矩阵。但是我们可以求解它的伪逆矩阵，尽管我们可以得到最终的求解结果，但是这并不是一个很好的假设函数h。
参考同济大学线性代数矩阵的秩定理7，XTX的秩小于等于X的秩，X的秩<=min(m,n),也就是说XTX的秩<=n，所以XTX作为n+1阶行列式为0，矩阵不可逆。

幸运的是，正则化的求解方法考虑到了这一情况，只要我们保证λ是大于0的，我们就可以确信上图中求逆矩阵的部分是可逆的。因此通过正则化这一操作，也可以解决一些X^TX出现不可逆的问题。这样我们就能很好地对一个很小的训练集但拥有大量的特征的训练集使用线性回归。

14.4 Logistic回归的正则化

对于逻辑回归，我们提到过两种优化方法，一种是使用梯度下降，另一种是更高级的优化方法。这些算法都需要你去想办法计算代价函数J(θ)，想办法去计算函数的导数。在本节中，我们将会展示如何改进这两种算法，使得它们都能够应用于正则化逻辑回归中去。

14.4.1 使用正则化的梯度下降算法

前面13我们提到，逻辑回归也会遇到过拟合的情况，尤其是当我们使用高阶多项式去拟合数据的时候。通常情况下，如果逻辑回归中有很多特征，有无关紧要的多项式。这些大量的特征，最终会导致过拟合的现象。
在逻辑回归中，我们定义的代价函数如下：

$$J(\theta)=\frac{1}{m}\sum_{i=1}^mCost(h_\theta(x^{(i)}),y^{(i)})$$ $$Cost(h_\theta(x),y)=-ylog(h_\theta(x))-(1-y)(1-h_\theta(x))$$

为了使用正则化，我们需要对上式进行一些修改，拟合函数如下图：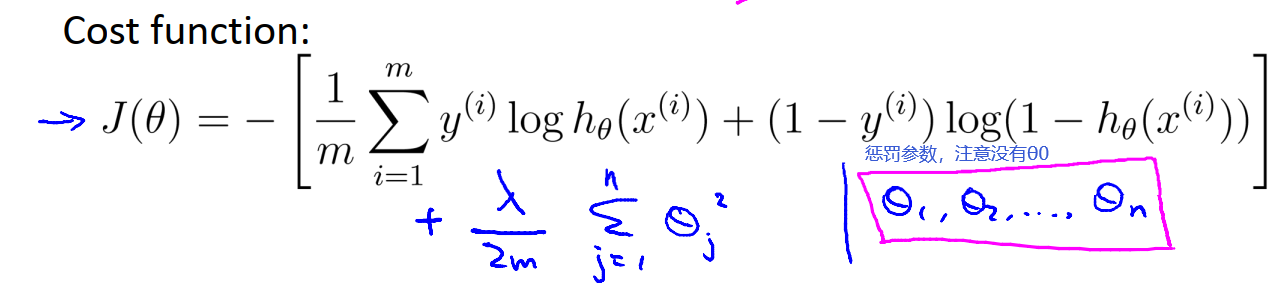

这样做的话，产生的效果就是，即使当你拟合阶数很高，且参数很多，只要添加了这个正则化项，保持参数较小，就仍然可以得到一条比较平滑的决策边界。使用正则化的效果就是即使我们有很多特征，正则化都可以帮助我们避免过拟合的现象。
我们添加正则化项之后的梯度下降算法如下图：

14.4.2 使用正则化的高级优化算法

对于这些高级优化算法(13中)，我们需要自己定义一个costFunction函数，这个函数以参数向量θ作为输入。然后将他赋值给fminunc函数中的参数，fminunc函数的功能是在无约束条件下求最小值，它会将costFunction最小化。
costFunction会返回两个值，第一个是jVal，因此我们需要一部分代码来计算代价函数J(θ)，在下图中，表明了应用正则化方法代价函数J(θ)需要进行的改变。cost Function函数的另一个返回值是梯度向量。

我们对costFunction函数调用fminunc函数或者其他类似的高级优化函数，这将最小化新的正则代价函数J(θ)，而函数的返回参数代表的就是正则化逻辑回归的解。
逻辑回归是线性分类器，接下来将会了解到一些非线性的分类器。
学习进度

15 逻辑回归实现

15.1 线性可分知识点回顾

我们使用逻辑回归实现二分类。二分类问题又可以分为线性可分与线性不可分。线性可分是指我们可以大致使用一条直线对数据集进行划分。我们的第一个例子是线性可分的，第二个例子是线性不可分的。
现在我们先看第一个例子，我们的假设函数如下：

$$h_\theta(x)=g(X\theta)$$ $$h_\theta(x)=g(\theta_0+\theta_1x_1+\theta_2x_2)$$ $$g(z)=\frac{1}{1+e^{-z}}$$

激活函数g的作用是把假设函数h的值域从负无穷到正无穷压缩到了0到1之间。然后如果h≥0.5，那么输出y=1；如果h＜0.5，输出y=0。我们很容易发现，其实这与Xθ是大于0还是小于0有关。
我们将逻辑回归中的代价函数进行向量化，如下图：

我们的梯度更新原理为：

15.2 逻辑回归-线性可分 数据可视化

根据学生的两门学习成绩，预测该学生是否会被大学录取。

fig,ax = plt.subplots()
# 过滤出所有被接收的点
ax.scatter(data[data['Accepted']==0]['Exam 1'],data[data['Accepted']==0]['Exam 2'],c='r',marker='x',label='y=0')
ax.scatter(data[data['Accepted']==1]['Exam 1'],data[data['Accepted']==1]['Exam 2'],c='b',marker='o',label='y=1')
ax.legend()
ax.set(xlabel='exam1',ylabel='exam2')
plt.show()

15.3 损失函数

先定义激活函数：

def sigmoid(z):
    return 1/(1+np.exp(-z))

再定义损失函数：

def costFunction(X,Y,theta):
    inner = sigmoid(X@theta)
    first = Y*np.log(inner)
    second = (1-Y)*np.log(1-inner)
    # 累加每个样本点的误差
    return -np.sum(first+second)/len(X)

15.4 梯度下降、预测

梯度更新函数如下：

def gradientDescent(X,Y,theta,iters,alpha):
    size = len(X)
    costs = []
    for i in range(iters):
        theta = theta-X.T@(sigmoid(X@theta)-Y)*alpha/size
        cost = costFunction(X,Y,theta)
        costs.append(cost)
    return costs,theta

预测函数如下：

def predict(X,theta):
    prob = sigmoid(X@theta)
    # numpy语法，list迭代器
    return [1 if x>= 0.5 else 0 for x in prob]

计算精度的方法如下：

y_ = np.array(predict(X,theta_final))
y_pre = y_.reshape(len(y_),1)
# 规定参与计算均值的元素的条件
acc = np.mean(y_pre == Y)
print(acc)

15.5 决策边界

我们的决策边界是：

$$\theta_0+\theta_1x_1+\theta_2x_2 = 0$$

在绘图时，我们把x1当成横轴，把x2当成纵轴，那么我们的决策边界函数为：

$$x_2 = -\frac{\theta_0}{\theta_2}-\frac{\theta_1}{\theta_2}x_1$$

绘制决策边界的代码如下：

coef1 = -theta_final[0,0]/theta_final[1,0]
coef2 = -theta_final[1,0]/theta_final[2,0]
x = np.linspace(20,100,100) # 在20到100之间，生成100个点
f = coef1+coef2*x
fig,ax = plt.subplots()
# 过滤出所有被接收的点
ax.scatter(data[data['Accepted']==0]['Exam 1'],data[data['Accepted']==0]['Exam 2'],c='r',marker='x',label='y=0')
ax.scatter(data[data['Accepted']==1]['Exam 1'],data[data['Accepted']==1]['Exam 2'],c='b',marker='o',label='y=1')
ax.legend()
ax.set(xlabel='exam1',ylabel='exam2')
ax.plot(x,f,c='g')
plt.show()

15.6 逻辑回归-线性不可分 特征映射

我们解决线性不可分问题的方法是特征映射。见数据挖掘理论算法学习24。
我们需要决定根据芯片在两次测试中的测试结果，决定芯片是要被接受还是抛弃。
特征映射代码如下：

def feature_mapping(x1,x2,power):
    # 新建一个字典存放映射结果
    data = {}
    # 传入两个特征和要映射的阶次
    for i in np.arange(power+1): # 从0一直循环到power
        for j in np.arange(i+1): # 从0到i
            data['F{}{}'.format(i-j,j)] = np.power(x1,i-j)*np.power(x2,j)
    return pd.DataFrame(data) # 将字典型数据转换成dataFrame结构

x1 = data['Test 1']
x2 = data['Test 2']
data2 = feature_mapping(x1,x2,6)
data2.head()

15.7 加入正则化项的损失函数

我们构造数据集X时直接从data2中取出所需的特征即可，不需要对原数据集data进行切分，但对Y需要切片。

X = data2.values
X.shape
Y = data.iloc[:,-1].values
Y = Y.reshape(len(Y),1)
Y.shape

在加入正则化项之后的损失函数表达式为：

代码实现为：

def sigmoid(x):
    return 1/(1+np.exp(-x))
def costFunction(X,Y,theta,lamda):
    inner = sigmoid(X@theta)
    first = Y*np.log(inner)
    second = (1-Y)*np.log(1-inner)
    # 添加正则化项 对从1到后面所有的θ进行平方求和
    reg = np.sum(np.power(theta[1:],2))*(lamda/(2*len(X)))
    return -np.sum(first+second)/len(X)+reg
theta = np.zeros((28,1))
lamda = 1
cost_init = costFunction(X,Y,theta,lamda)
print(cost_init)

15.8 加入正则化项的梯度下降、准确率

在加入正则化项之后的梯度下降更新方式为：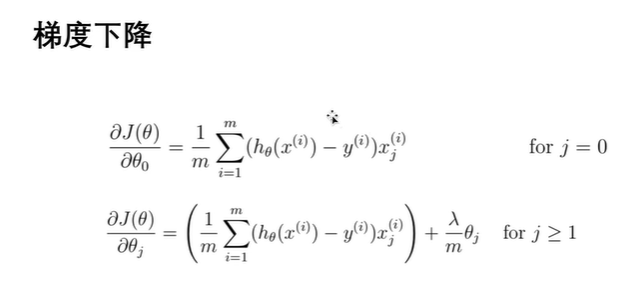

代码实现为;

def gradientDescent(X,Y,theta,alpha,iters,lamda):
    costs = []
    for i in range(iters):
        reg = theta[1:]*lamda/len(X)
        # 因为我们不对θ0进行任何操作，所以我们在reg第一行之前插入一行0
        # 因为我们是对全部列操作，所以axis = 0
        reg = np.insert(reg,0,values=0,axis = 0)
        theta = theta-(X.T@(sigmoid(X@theta)-Y))*alpha/len(X)-alpha*reg
        cost = costFunction(X,Y,theta,lamda)
        costs.append(cost)
        if i% 1000 == 0:
            print(cost)
    return theta,costs
alpha = 0.001
iters = 200000
lamda = 0.001
theta_final,costs = gradientDescent(X,Y,theta,alpha,iters,lamda)

准确率计算方式与线性可分的例子类似。

15.9 决策平面

绘制代码如下：

# 数据集本身的绘制
fig,ax = plt.subplots()
ax.scatter(data[data['Accepted']==0]['Test 1'],data[data['Accepted']==0]['Test 2'],c='r',marker='x',label='y=0')
ax.scatter(data[data['Accepted']==1]['Test 1'],data[data['Accepted']==1]['Test 2'],c='b',marker='o',label='y=1')
ax.legend()
ax.set(xlabel='Test1',ylabel='Test2')

# plt.contour(xx,yy,zz,0) 等高线是三维的，最后一个数据表示的是绘制的是数据为多少的等高线
x = np.linspace(-1.2,1.2,200) # 生成范围为-1.2到1.2的200个数据
xx,yy = np.meshgrid(x,x) # np中生成网格的函数,生成200*200的矩阵 就是图中x1轴和x2轴的数据
z = feature_mapping(xx.ravel(),yy.ravel(),6).values# 对xx和yy进行一个特征映射 ravel使得xx变成400*1的向量 最后加上values从dataframe变成array
# 我们需要的是zz=0的点，就是我们的分界面
zz = z@theta_final
# 此时zz是40000*1维的，我们需要把他变成200*200方便画图
zz = zz.reshape(xx.shape)
plt.contour(xx,yy,zz,0)
plt.show()

16 神经网络

16.1 非线性假设

神经网络是一个相对古老的算法。与线性回归和逻辑回归相比，神经网络具有复杂的非线性假设。对于很多机器学习问题，特征个数n是很大的，那么我们就会得到更多的交叉项。因此只是包括平方项或者立方项特征的简单逻辑回归算法，并不是一个在n很大时学习复杂的非线性假设的好办法，因为有过多的特征参与。神经网络在学习复杂的非线性假设上被证明是一种好得多的算法，即使输入特征空间或n很大。

16.2 模型展示-如何表示模型

神经网络的起源是人们尝试设计出模仿大脑的算法。神经元是一个计算单元，他从输入通道接收一定数目的信息并做一些计算，然后将结果通过它的输出通道传送到其他节点。
我们将神经元模拟成一个逻辑单元。如下图：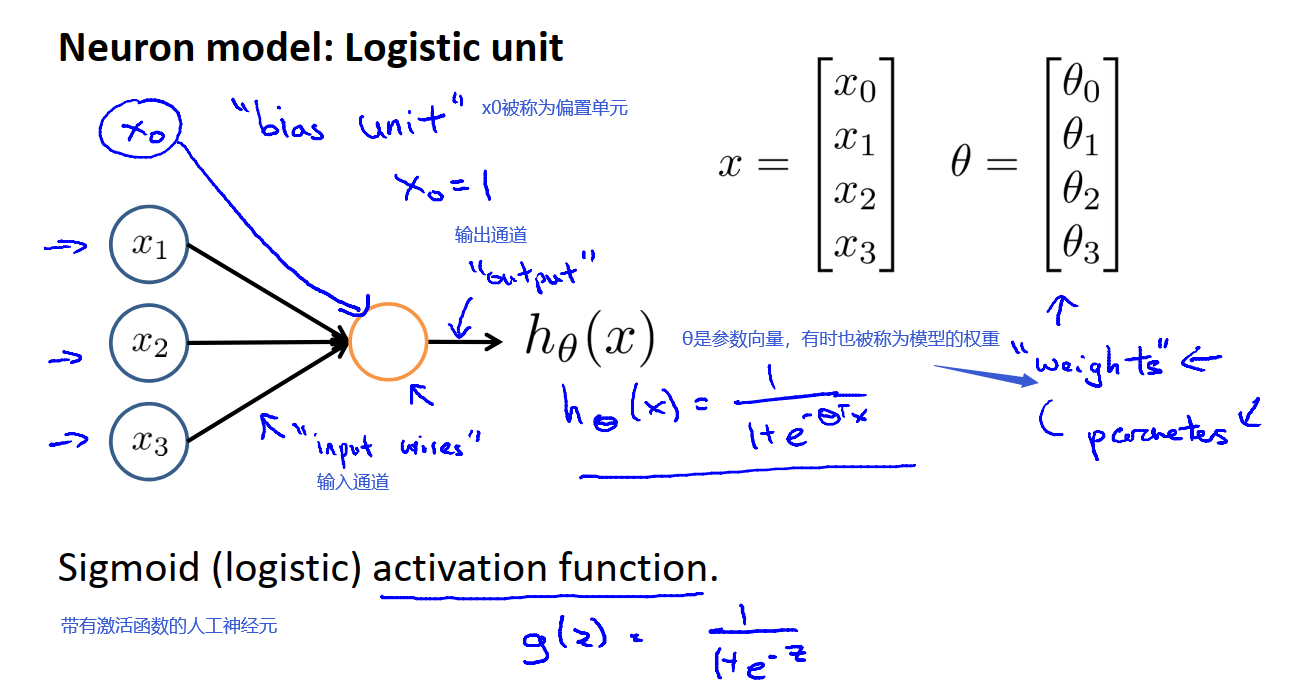

神经网络实质上就是一组神经元连接在一起的集合。如下图：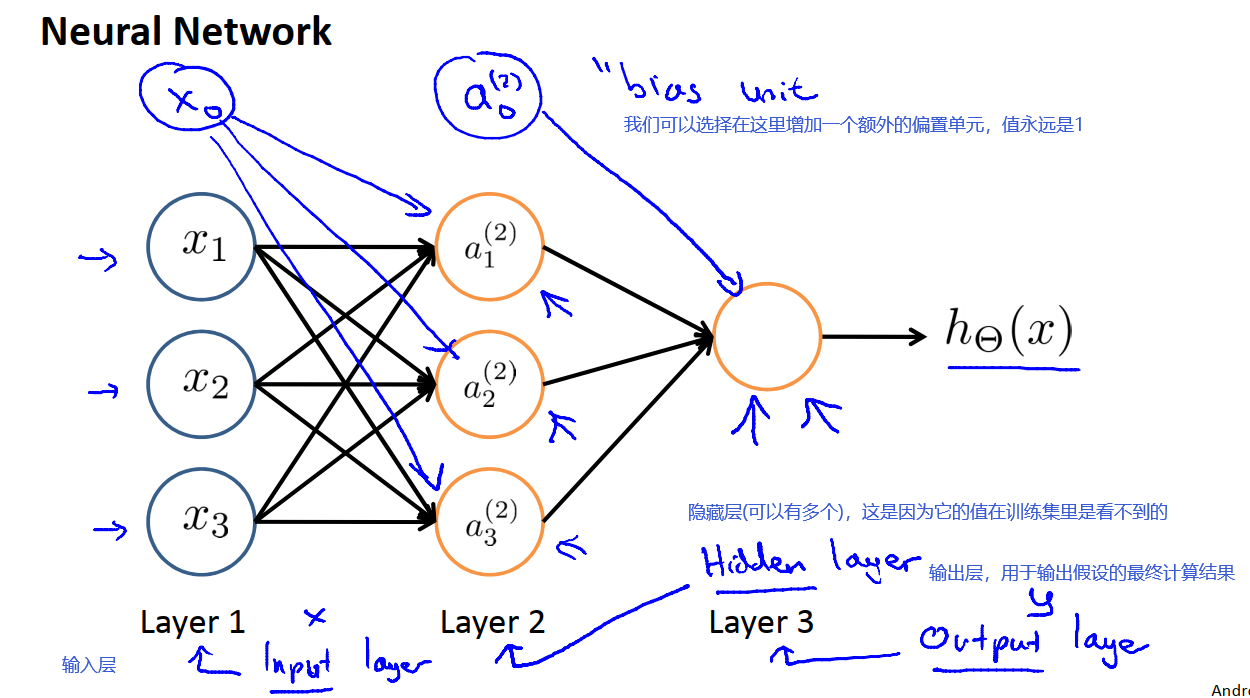

下面我们解释神经网络具体的计算步骤，其中：
ai^j表示第j层第i个神经元的激活项。激活项是指由一个具体的神经元计算并输出的值。
θj是一个权重矩阵，它控制从第j层到第j+1层的映射。θ上标表示第i层的特征矩阵，θ下标是矩阵row和column。第一层到第二层为θ1，第二层到第三层为θ2。θ1具体情况如下图：(请注意没有第一行，偏置单元没有权重)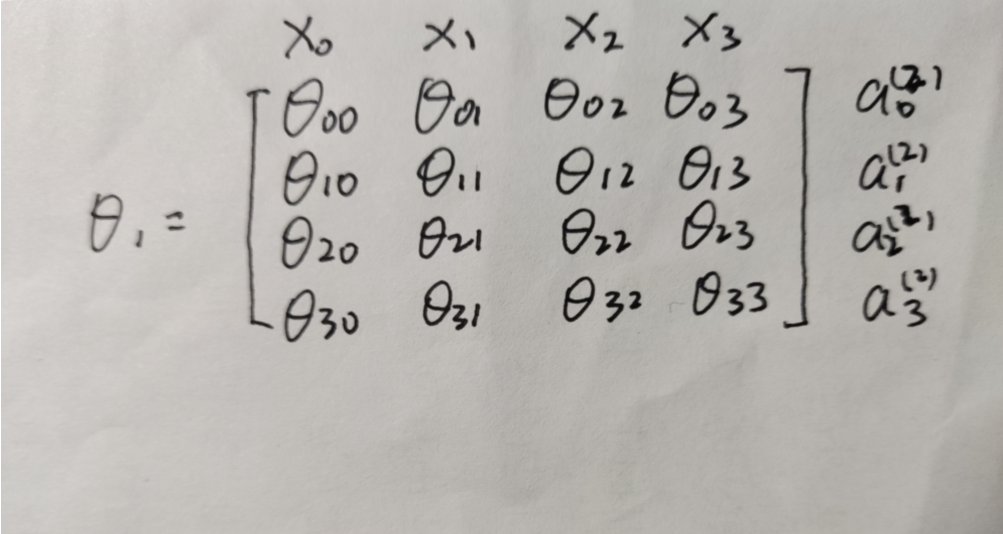

具体计算过程见下图：

如果神经网络在j层有s(j)个单元，在j+1层有s(j+1)个单元,则θj矩阵的维度为s(j+1)×(s(j)+1)，因为j层还有一个x0。
一个人工神经网络定义了函数h，从输入x到输出y的映射。这些假设函数被参数化，我们将参数记为Θ，这样一来改变Θ，就能得到不同的假设函数，也就有了输入x到输出y的多种映射方式。

16.3 神经网络模型向量化实现

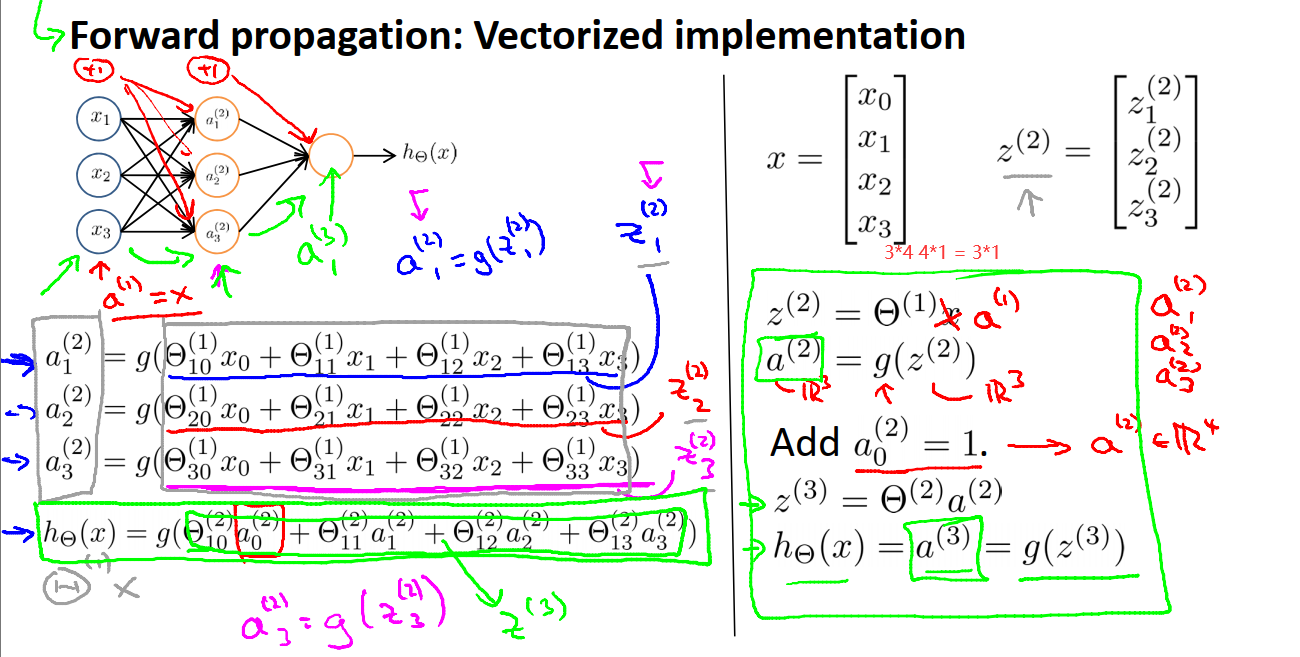
上图中的z，都是该层输入x0，x1，x2，x3的加权线性组合。z值可以通过矩阵向量乘法来得到。根据这个，我们就可以将神经网络的计算向量化了。为了便于统一表示，我们将输入层的接收到的输入看成是第一层的激活项(即第一层的计算结果)，例如我们定义a^1 = x,所以a^1就是一个向量了，所以有z^2 = Θ^1 a^1。
接下来我们额外加上一个a^2_0 = 1,注意偏置单元没有权重θ，因此θ2的维度为3*4，a^2的维度为4*1。
上图中右边为计算h(x)的过程，也被称为前向传播，这是因为我们从输入单元的激活项开始，然后进行前向传播给隐藏层，计算隐藏层的激活项，然后我们继续前向传播并计算输出层的激活项。这个依次计算激活项，从输入层到隐藏层再到输出层的过程叫前向传播，我们谈到的是这一过程的向量化实现方法。
这种前向传播的方法也能帮助我们理解神经网络的作用和它为什么能够帮助我们学习有趣的非线性假设函数。在下图所示的神经网络中，如果我们暂时遮盖住它的输入层，我们会发现图中剩下的部分看起来很像逻辑回归。也就是以汇点为逻辑回归单元来预测h(x)的值(即把左边三个神经元看成x，中间那个圈堪称是sigmoid函数)，我们的假设函数就是图中的h(x)。θ_{10}可以理解成上一级a0的计算结果在下一级a1中的权重。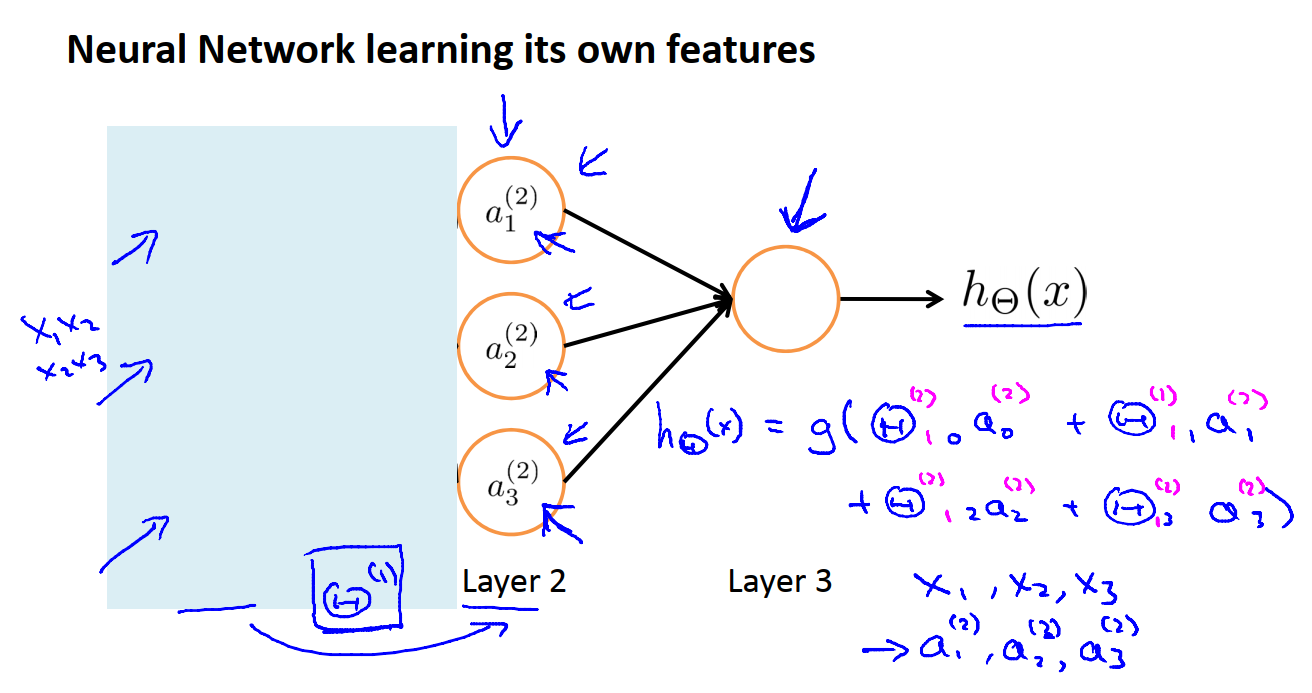

这实际上就是逻辑回归，但是逻辑回归模型中输入的特征，是通过隐藏层计算的这些数值。这个神经网络所做的事情，就像是逻辑回归，但是它不是使用原本的x1，x2，x3作为特征，而是使用a1，a2，a3作为新的特征。所以这本质上是一个特征工程。从原始数据X挖掘出一层比一层有用的特征A1, A2, … 最后使用逻辑回归线性拟合得出预测。而挖掘特征时使用的方法也是逻辑回归。
神经网络中神经元的连接方式，又称为神经网络的架构。架构是指不同的神经元的连接方式。如下图：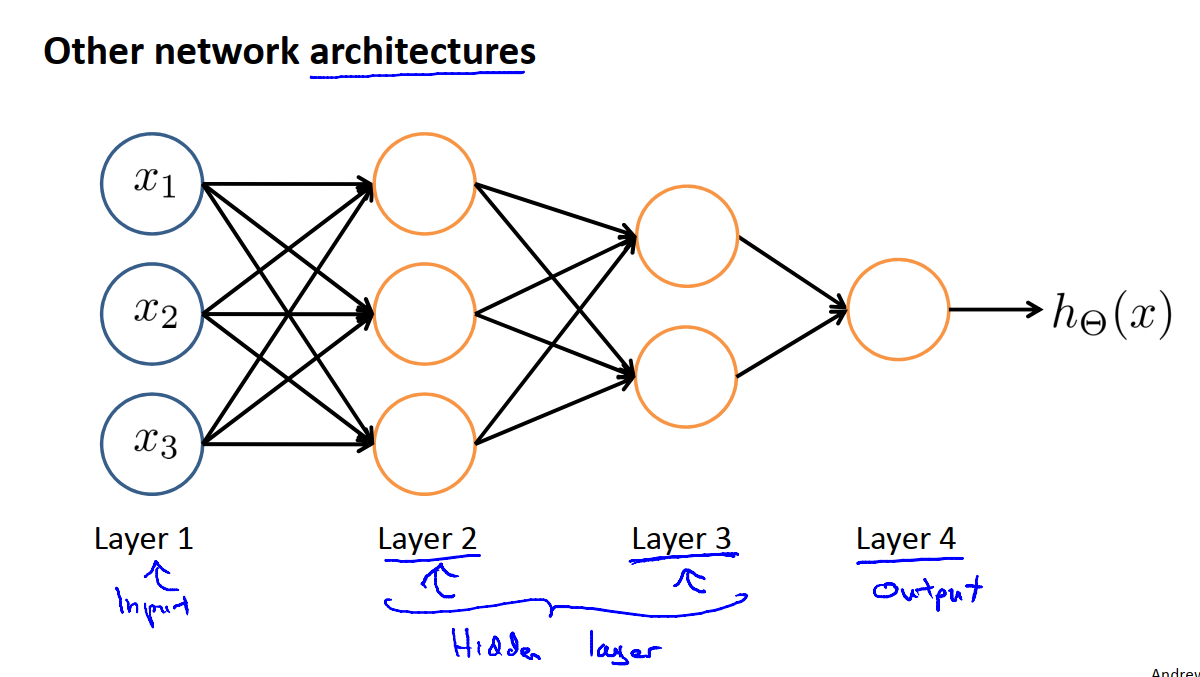

第二层有三个隐藏神经元，它们会计算一些输入层的复杂功能，然后第三层可以将第二层训练出的特征项作为输入，然后在第三层计算出更复杂的特征。因此在第四层时就可以利用在第三层训练出的更复杂的特征作为输入，以此得到非常有趣的非线性假设函数。第一层被称为输入层，第四层被称为输出层，这个网络有两个隐藏层。

16.4 含有一个神经元的网络

在本节中，我们通过一个详细的例子来说明神经网络是怎样计算复杂非线性函数的输入的，为什么神经网络可以用来学习复杂的非线性假设模型。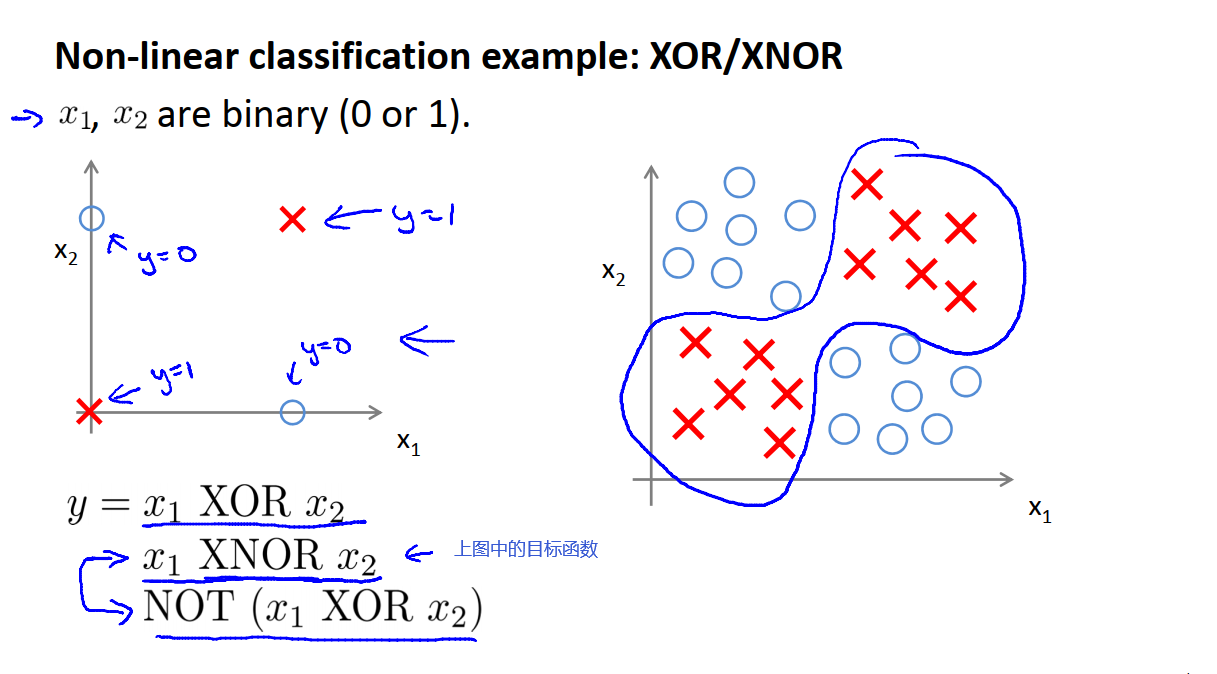

上图中，x1，x2的取值范围为0，1。左图可以看成是右图复杂机器学习问题的一个简化版本，我们的目标是去学习一个非线性的判断边界来区分这些正样本和负样本。

16.4.1 拟合AND

为了建立能够拟合XNOR运算的神经网络，我们先从一个比较简单的能够拟合AND运算的网络入手。
假设有两个二进制的输入x1和x2，只能取0或1，现在目标函数y = x1 AND x2，and的意思是逻辑与。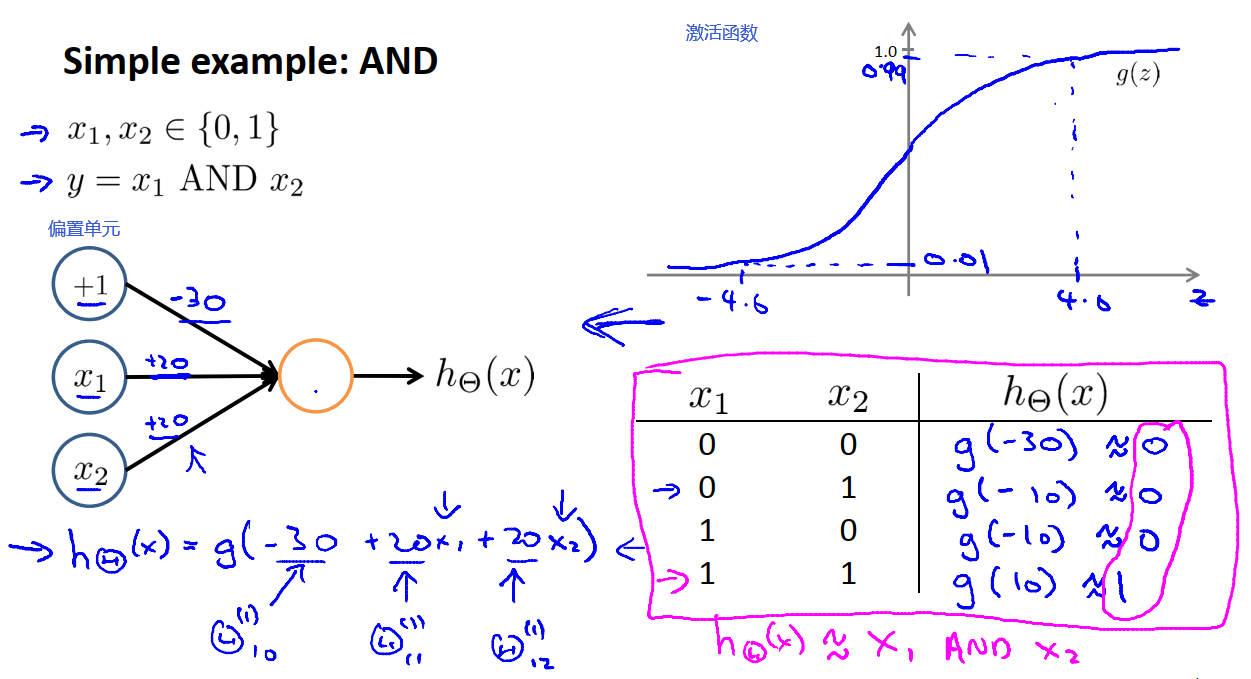

现在我们对上图网络中的权重或者说参数进行赋值，权重标在图中对应边上。由此我们可以写出图中底部位置的假设函数。把图中θ都想成是网络边界中连接着这些输入参数的权值。然后我们带入具体的x1和x2的值观察神经元的输出结果，见上图右侧部分。

16.4.1 拟合OR

下图中的神经网络可以实现OR的功能。

通过上面的例子我们可以明白神经网络中的单个神经元是如何被用来计算逻辑函数，事实上线性可分的问题可以用单个神经元完成，也就是一个逻辑回归。

16.5 含有多个神经元的网络

16.5.1 not函数(非)

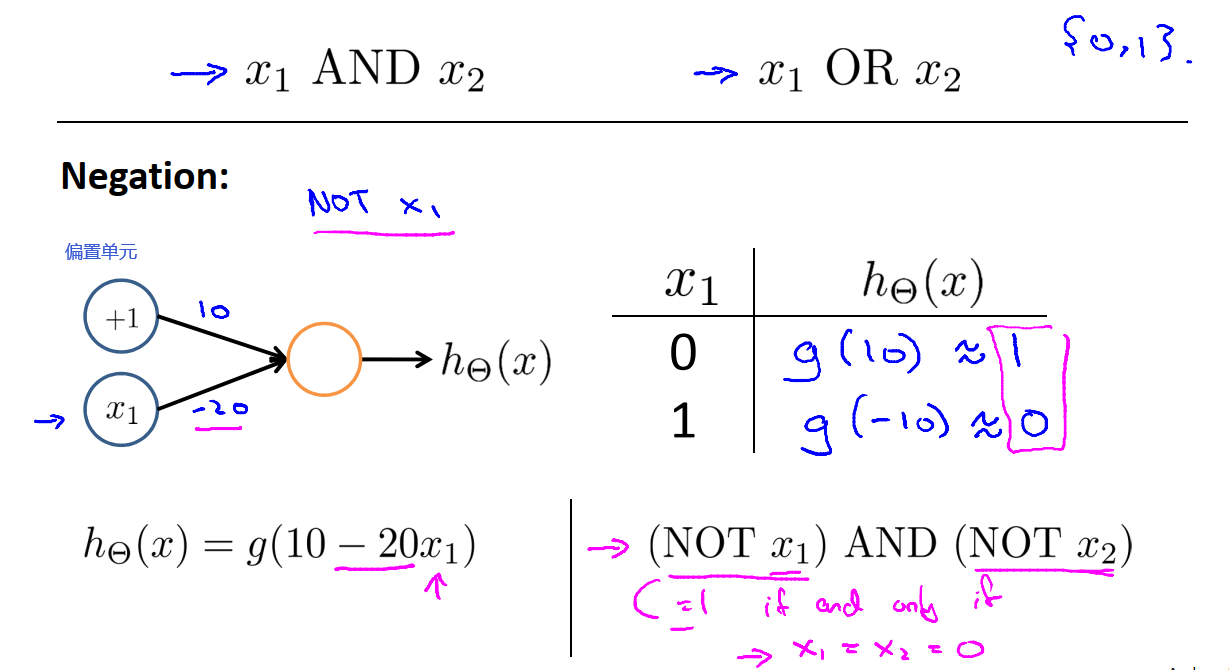
实现非逻辑的思想就是在预期得到非结果的变量前面放一个很大的负权重，如上图中的-20。

16.5.2 xnor函数(异或非)

在实现了与、或、与非的基础上，我们就可以实现xnor逻辑，具体实现如下图。很显然我们需要一个非线性的决策边界。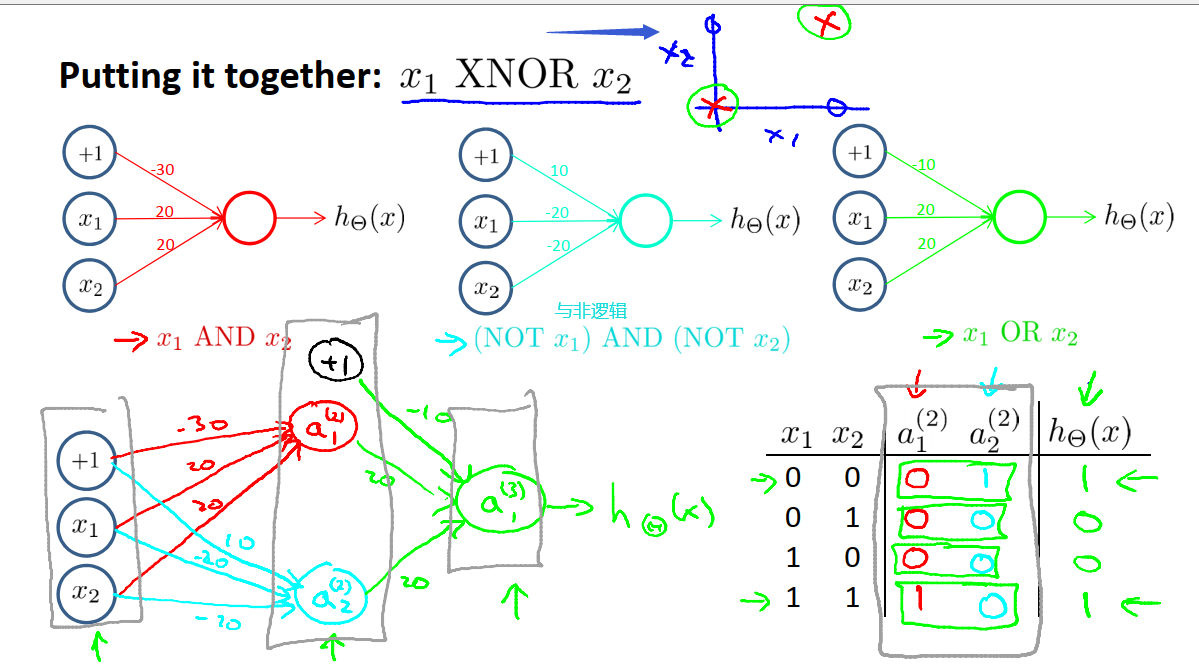

我们的输入都放在输入层，然后在中间放一个隐藏层，用来计算一些关于输入的略微复杂的功能，然后再继续增加一层，用于计算一个更复杂的非线性函数，这就是为什么拥有很多层的神经网络可以计算这种复杂的函数。

16.6 使用神经网络的多元分类

要在神经网络中实现多分类，采用的方法本质上是逻辑回归中一对多法的拓展，我们需要用到4个逻辑回归分类器。例如我们想要实现一个四分类模型，实现对行人、小汽车、摩托、卡车的分类，我们需要建立一个有四个输出单元的神经网络，即神经网络的输出为一个四维向量，我们要做的是利用第一个输出单元判断图中是否是一个行人，再用第二个输出单元来判断图片中是否是一辆汽车，再用第三个输出单元来判断是否是一辆摩托，最后用第四个输出单元来判断图中国是否是一辆货车。如果输入的是一个行人的照片，理想的输出是1 0 0 0，其他类别以此类推。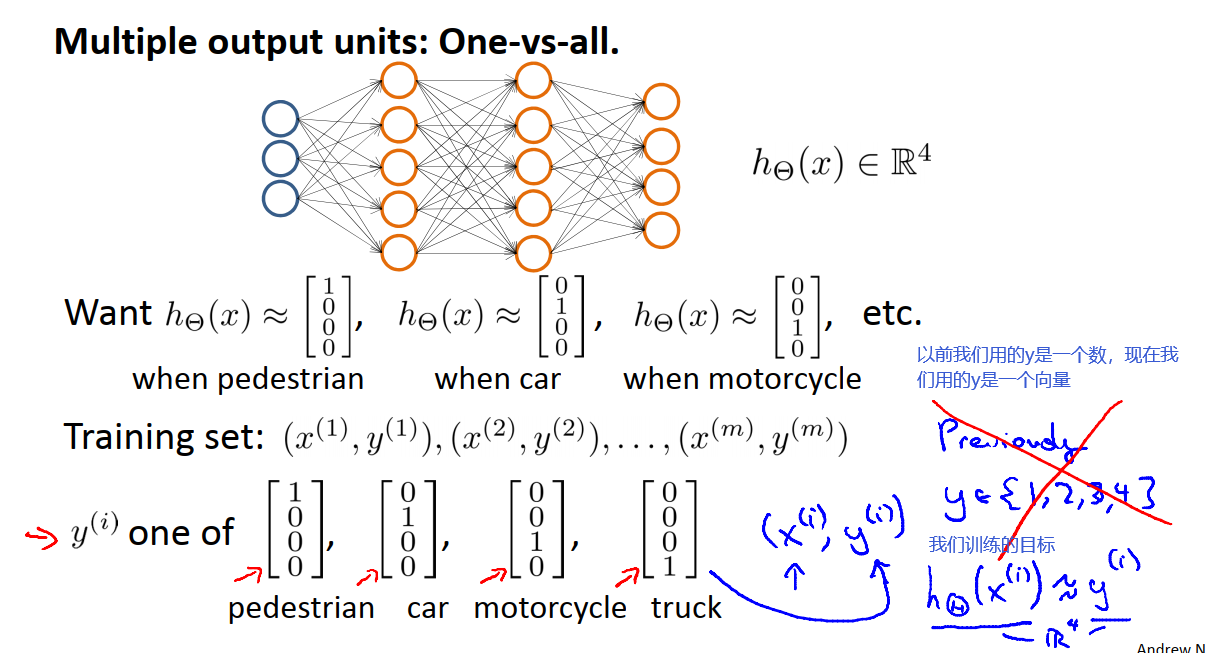

16.7 代价函数

接下来我们来了解一个学习算法，它能在给定训练集时，为神经网络拟合参数。我们将从拟合神经网络参数的代价函数开始谈起。
我们问题的背景是神经网络在分类问题中的应用。
L表示神经网络中的总层数，对于上图的神经网络，L = 4。
s_l表示第l层的单元数，也就是神经元的数量，这其中不包括第l层的偏置神经元。例如，s_1 = 3,s_2 = 5。
我们考虑两种情况的分类问题，第一种是二元分类，这里y只能为0或是1，在这种情况下我们会有一个输出单元，也就是计算出来的h(x),它将会是一个。在这种情况下s_l是输出单元的个数，其中L代表最后一层的序号，s_l = 1,二分类问题的k值为1，也就等于输出层的单元数目。
第二种分类问题是多分类问题，也就是说会有k个不同的类。之前的例子中，如果我们有四类的话，我们就使用一个四维向量来表示y。那么k个输出单元(s_l = k,k≥3)，我们的假设函数就会输出k维的向量。只有k≥3时我们才需要使用这种一对多的方法，如果只有2个类别，我们只需要一个输出单元就可以了。
在神经网络中我们使用的代价函数是逻辑回归中使用的代价函数的一般形式。即y由一个数变成了一个向量，这是因为神经网络现在的输出变成了一个k维向量。代价函数见下图：

16.8 反向传播算法

上一节中我们了解了神经网络的代价函数J(θ)，接下来我们寻找使得J(θ)最小化的方法。为了使用梯度下降算法或者其他某种高级优化算法，我们需要做的是写代码获得输入参数θ，并计算J(θ)和对θij的偏导项。J(θ)可以直接通过定义式计算得到。因此我们关注的地方是偏导数的计算。
首先我们再次解释一下神经网络前向传播的过程，如下图：

向量化使得我们可以计算神经网络结构里的每一个神经元的激活值。接下来，为了计算导数项，我们将采用一种叫做反向传播(backpropagation)的算法。
反向传播算法从直观上说就是对每一个节点我们计算δ^l_j,就用这种方式代表了第l层的第j个节点的误差。前面我们提到，a^l_j表示的是第l层第j个单元的激活项。所以这个δ值，在某种程度上就捕捉了我们在这个神经节点的激活值的误差，所以我们可能希望这个节点的激活值稍微不一样。
具体地讲，我们用右边这个有四层的神经网络结构做例子。所以第4层第j个单元的δ^4_j = a^4_j - y_j,即该单元的激活值减去训练样本里的真实值，其中a^4_j也可以写成hθ(x)_j,这里的下标j是输出向量中第j个元素的值。如果我们把上式中的δ^4_j = a^4_j - y_j这三项都看成向量，式子就变成了δ^4 = a^4 - y，并且向量维度等于输出单元的数目。所以现在我们得到了第四层的误差项δ^4。δ^3的向量化计算方式如下：

$$\delta^{(3)} = (\theta^{(3)})^{T}\delta^{(4)}.*g'(z^{(3)})$$

其中.*是点乘。g’(z^3)其实是对激活函数g在输入值为z(3)的时候所求的导数。因为激活函数的导数为

$$\frac{\partial g(z)}{\partial z} = g(z)(1-g(z))$$

所以有：

$$g'(z^{(3)}) = g(z^{(3)}).*(1-g(z^{(3)})) = a^{(3)}(1-a^{(3)})$$

其余δ的计算方式见下图：

反向传播这个名字源于我们从输出从开始计算δ项，然后我们返回到上一层计算第三隐藏层的δ项，接着我们再往前一步来计算δ2，所以说我们是类似于把输出层的误差反向传播给了第3层，然后是再传到第2层，这就是反向传播的意思。
最终我们可以得到偏导数项的计算式为：

$$\frac{\partial J(\theta)}{\partial \theta_{ij}} = a^{(l)}_j\delta^{(l+1)}_i$$

在上式中我们忽略了λ或者说标准化项，也就是λ项=0。我们将在之后完善正则项细节。

在上图中，我们首先初始化偏导数数组Δij，将它的初值都设为0。我们打算使用这个数组来计算偏导数。所以这些δij被作为累加项慢慢地增加，以计算出所有的偏导数项。
解析来我们将遍历我们的训练集。对于第i个循环而言，我们将取第i个训练样本x^i和y^i。
于是我们要做的第一件事是设定a^1向量(即输入层的激活函数)，设定它等于x^i。
接下来我们运用正向传播，来计算第二层、第三层一直到第L层的激活值。
接下来，我们将用我们这个样本的标签值y^i来计算模型输出值对应的误差项δij，所以δ^L就是假设的输出值a^L减去模型的目标输出值y^i。
接下来，我们打算运用反向传播算法来计算δ(L-1)、δ(L-2)一直到δ(2),再强调一下，这里没有δ(1),因为我们不需要对输入层考虑误差项。
最后我们将用这些Δij来累加我们在前面计算好的篇导数项δij。我们也可以把这个过程向量化，具体来说，如果把δij看作一个矩阵，ij表示矩阵中的位置。如果δ(L)是一个矩阵，我们就可以把求累加和的操作写成图中红框部分的式子，实质上就是使得第i行δ乘上第j列a。其中δ(l+1)的维度是(第l+1层神经元的个数)(第l+2层(或是要求输出的类)神经元的个数)，a(l)的维度是(第l层的神经元的个数)\(第l+1层神经元的个数)，所以是满足矩阵乘法规则的。
最后我们跳出这个for循环，计算最下面的两个式子得到Dij，当j=0时，对应偏差项，当j≠0时，我们加入正则化项。Dij就是J(θ)关于每个参数的偏导数，然后我们可以使用梯度下降或者其他高级优化算法。

16.9 理解反向传播

在本小节中，我们更多地关注一下反向传播的一些固定步骤，说明这些固定步骤在做什么。
我们从前向传播开始，如下图：

神经网络的前向传播过程如下图：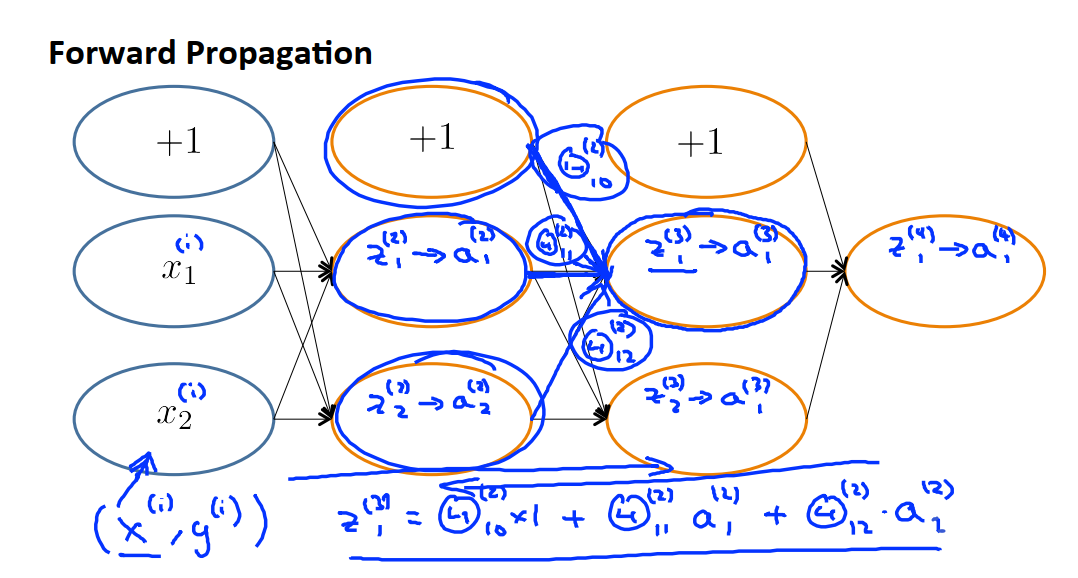

事实上，下文中我们会发现，反向传播的过程和前向传播非常相似，只是这两个算法计算的方向不一样而已。在反向传播中，是从右往左进行运算，并且计算方法和前向传播非常相似。
为了更好地理解反向传播算法的过程，让我们先看看代价函数，我们关注于一个样本x^i,y^i,且神经网络只有一个输出单元并且忽略正则化项(λ=0)的情况。如下图：

首先我们观察代价函数J(θ)对应于第i个样本的值，即中括号内的求和项。这个代价函数扮演一个类似方差的角色，我们可以把cost(i)近似地当成神经网络输出值h(x)与实际值y^i的方差。就像逻辑回归实际中会偏向于选择比较复杂的，带对数形式的代价函数，但为了方便理解，可以把这个代价函数看作是某种方差函数。因此cost(i)表示了神经网络预测样本的准确程度，也就是网络的输出值和实际观测值y^i的接近程度。

16.9.1 δ项的意义

如下图，反向传播算法就是在计算这些δ^l_j项，我们可以把它看作是我们在第l层中第j个单元中得到的激活项和目标值的误差。更深入地来说，δ项实际上是代价函数cost(i)关于z^l_j的偏导数，也就是计算出的上一层a项的加权和，或者说代价函数关于z项的偏导数。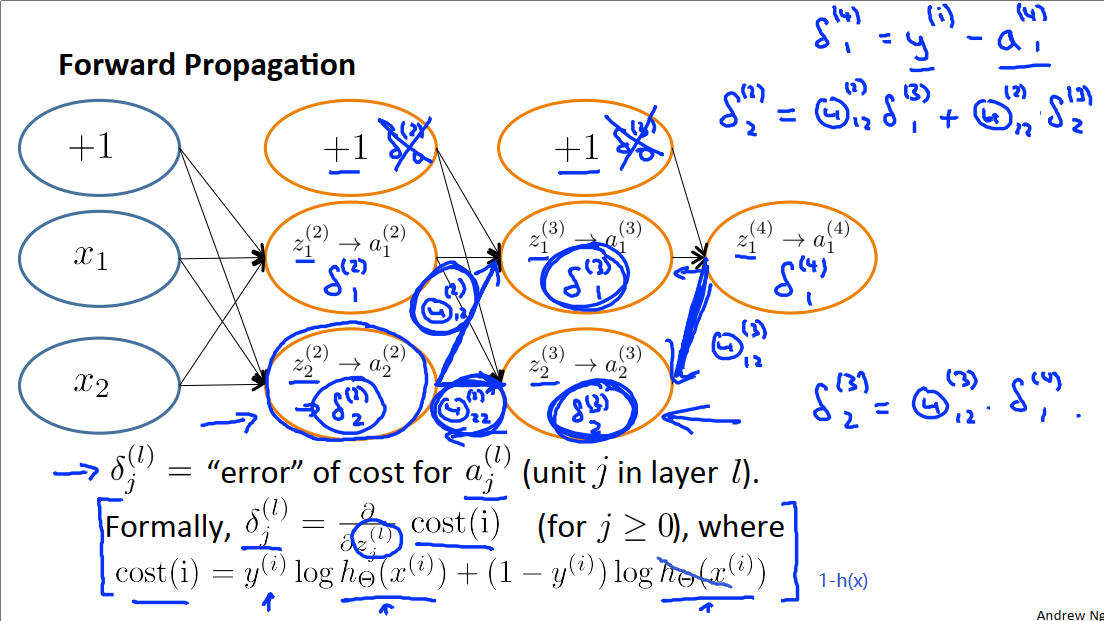

具体来说，代价函数是一个关于标签y和神经网络中h(x)的输出值的函数，如果分析网络的内部，稍微把z^l_j改一下，就会影响到神经网络的h(x),最终将改变代价函数的值。
综上，δ项实际上是代价函数关于这些计算得出的中间项的导数，他们衡量的是为了影响这些中间值，我们需要改变神经网络中的权重的修改程度，进而影响整个神经网络的输出h(x),并影响所有的代价函数。
举个例子：f(x,y)=5x+3y,则对x求偏导就是5，它得到的是x的系数，即这里的权重参数。

16.9.2 δ项的计算方式

如上图，对于输出层，如果我们设δ比如δ^4_1,则它的计算方式是y^i-a^4_1,然后我们进行反向传播，计算过程稍后再解释，最后可以计算出前一层的δ项，也就是δ^3_1,δ^3_2,然后继续进行传播，最后计算出δ^2_1,δ^2_2,反向传播的计算过程和前向传播非常地相似，只是方向反了过来。我们以计算δ^2_2为例，与前向传播相似，我们要先标出一对权重，δ^3_1的权重是θ^2(12)(在前向传播时用到了，即第2层第2个神经元到第3层第1个神经元的权重),δ^3_2的权重是θ^2(22)。然后计算δ^2_2我们要做的是用δ^3_1*θ^2(12)，δ^3_2*θ^2(22),实际上就是后一层δ的加权和，加权是由对应边的强度来进行加权。
再来一个例子，我们要计算δ^3_2 = θ^3(12)*δ^4_1。
我们最后计算偏置单元的δ值，但是我们会忽略掉它们，并不使用，因为他们最后并不影响偏导数的计算。

16.10 实现-展开参数

在本节中，我们关注于怎样把我们的参数从矩阵展开成向量，以便我们在高级优化步骤中使用。

在上图中，首先我执行了代价函数，输入参数是θ，函数返回代价值以及导数值。
然后我们将返回值传递给高级优化算法fminunc，fminunc并不是唯一的算法，也可以使用别的优化算法，但它们的功能都是取出这些输入值，包括costFunction的函数指针，以及θ值得一些初始值，并且这些程序都假定θ和这些θ的初始值都是参数向量，也许是n或者n+1维。但它们都是向量。同时假定这个代价函数的第二个返回值，也就是梯度值也是n维或n+1维的，所以它也是一个向量。
下面的语句在我们使用逻辑回归的时候没有问题，但现在我们用神经网络，我们的参数不再是向量了，而是矩阵了，因此对于一个完整的神经网络，我们的参数矩阵为θ^1,θ^2,θ^3三个矩阵。
同样地这些梯度项，也是需要得到的返回值，对于四层的神经网络，我们的还需要的参数矩阵为D^1,D^2,D^3。
接下来，我们要谈到如何取出这些矩阵并将它们展开成向量，以便它们最终成为恰当的格式，能够给fminunc传入正确的θ，并且得到梯度的返回值。

如上图，假设我们有这样一个神经网络，其输入层有10个输入单元，隐藏层有10个单元，最后输出层只有一个输出单元。
在这种情况下，矩阵θ的维度和矩阵D的维度都确定了下来。θ^l = s(l+1)(s(l)+1)，即行数和下一层的单元数有关，列数是上一层单元数加一。然后我们把这些矩阵全部展开成n\1维的向量，如果有需要，我们还可以将它们返回到矩阵形式，使用的方法为reshape。

接下来我们将这一方法应用于我们的学习算法。如上图，首先我们有一些初始参数θ^1,θ^2,θ^3三个矩阵。
我们要做的是取这些参数然后把它们展开为一个长向量，然后作为θ参数的初始设置传入优化函数fminunc。
我们要做的另一件事是实现代价函数。代价函数会得到输入参数θ向量，它是所有的θ参数都展开成一个向量的形式。因此我要做的第一件事是使用θvec和重组函数reshape，将θvec变回θ^1,θ^2,θ^3三个矩阵，这样我就有了一个使用这些参数的更方便的形式。然后执行前向传播和反向传播来计算导数以及计算代价函数J(θ)。最后我们把计算得到的导数值也展开成与θvec对应的向量，并由代价函数返回。
使用矩阵表达式的好处是当你的参数以矩阵的形式存储时，在进行正向传播和反向传播时可以更加方便。且将参数存储为矩阵时，也更容易充分利用向量化实现。
使用向量表达式的优点是如果有像θvec或者Dvec这样的矩阵，在使用一些高级的优化算法时，这些算法通常要求把所有的参数要形成一个长向量的形式。

16.11 梯度检测

在上文中，我们讨论了使用前向传播和反向传播来计算导数。但是反向传播算法含有许多细节，因此实现起来比较困难。并且它有一个不好的特性，很容易产生一些微妙的程序错误。当它与梯度下降或是其他算法一起工作时，看起来它确实能正常运行，并且代价函数J(θ)在每次梯度下降的迭代中也在不断减小，虽然在反向传播的实现中存在一些程序错误，但程序运行状况看起来确实不错。这些程序错误不影响J(θ)的不断减小，但是到了最后，我们得到的神经网络，它的误差将会比没有错误的神经网络高出一个量级。并且我们很可能不知道得到的结果是由程序错误所导致的。
有一种思想叫做梯度检验，它能解决几乎所有这种问题，在神经网络实现反向传播或者类似梯度下降算法时，都需要使用梯度检验。它将会完全保证模型的前向传播以及后向传播都会是百分之百正确。程序错误之所以出现，绝大多数都和反向传播的错误实现有关。
当我们使用梯度检测方法时，我们可以自己去验证代码确实能正确计算出代价函数的导数。考虑下图中的例子，假设有一个代价函数J(θ)，并且有一个θ值(在图中注明了，我们假设θ是一个实数)，该点的导数就是图像在该点上切线的斜率。现在我们从数值上来逼近它的导数，或者说这是从数值上来求近似导数的方法，首先计算出θ+epsilon，它在θ的右边一点点，然后再计算出θ-epsilon，现在要做的是把这两个值对应的点用直线连起来，这条直线的斜率就是我们所求的该点导数的近似值，它真正的导数是θ这个点对应切线的斜率。数学上这条红线的斜率等于该段的垂直高度除以该段的水平宽度，因此θ点导数的近似值如下图红框中的内容。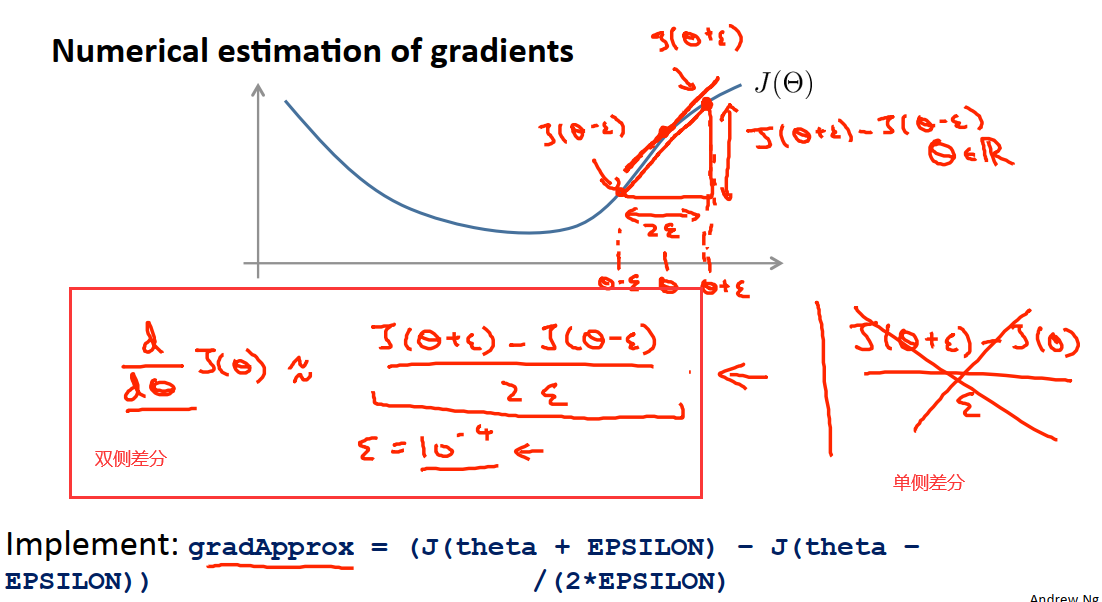

通常来说，epsilon是一个很小的值，大概是10^(-4)量级，也可以是其他的值。如果epsilon足够小，从数学上来讲，它就变成了该点真正的导数，成了函数在θ点上的切线的斜率。但是我们不会想去使用太小的epsilon值，因为这样回引发很多数值问题，所以我们通常取epsilon为10^(-4)量级的数。
上图中，双侧差分能得到更加准确的结果，所以相比单侧差分，我们通常都用双侧差分。
在前面，我们只考虑了θ是实数的情况，现在我们要考虑更普遍的情况——当θ为向量参数的时候，设θ是一个n维向量，他可能是神经网络中参数的展开模式。如下图：

所以θ是一个有n个元素的向量，从θ1到θn，我们可以用类似的思想来估计所有的偏导数项。具体来说，一个代价函数关于第一个参数θ1的偏导数可以通过增加J中的θ1参数(θ1+epsilon、θ1-epsilon)其余参数不变来求得，具体方式见上图。
上图中的这些等式能让我从数值上去估算代价函数J所关于任何θ的偏导数。
为了达到这一目的，我们需要实现下图中的代码;

假设i的值为1到n，这里的n是参数向量θ的维度，我们通常用它来计算展开形式的参数，因为θ只是神经网络中所有参数的一个列表。
先使θPlus=θ。
然后使得第i个θPlus加上epsilon，这样做就是使所有的θPlus项都赋上θ的值再加上epsilon值。这两行代码在加上epsilon的同时保证了其余θ参数不变。
下面的两行代码对θMinus进行类似的操作，只不过变成了减去epsilon。
最后，计算出梯度的近似值，就能近似得到J(θ)关于θi的偏导数的值。
我们在神经网络中使用这种方法时使用了for循环来完成我们对神经网络中代价函数的所有参数的偏导数的计算，然后与我们反向传播中得到的梯度进行比较，DVec是我们从反向传播中得到的导数，反向传播是计算代价函数关于所有参数的导数或者偏导数的一种有效方法，接下来通常要做的是验证这个计算出的导数是否和我们的近似值接近。如果这两种方法计算出的导数是一样的，或者说非常接近，那么我们就可以确信反向传播的实现是正确的。当我把向量DVec用到梯度下降中或者其他高级优化算法中时，我就可以确信我所计算的结果是正确的，他能很好地优化J(θ)。
最后我们总结一下梯度检验的全部过程：
1 通过反向传播计算Dvec。他可能是D^1,D^2,D^3这些矩阵展开的形式。
2 实现数值上的梯度检验，计算出gradApprox。
3 确保Dvec与gradApprox都能得出相似的值。
4 最关键的一步，在使用代码进行学习或者训练网络之前，重要的是关掉梯度检验。这是因为梯度检验的代码是一个计算量非常大的、运行非常慢的计算导数的程序，而我们之前提到的反向传播算法(即计算Dvec的算法)它是一个高性能的计算导数的方法，一旦我们通过检验确定反向传播的实现是正确的，就应该关掉梯度检验。如果我们在每次梯度下降迭代或者在每次代价函数的内循环里都运行一次梯度检验，程序就会变得非常慢。

16.12 随机初始化

当你执行一个算法，例如梯度下降算法或者高级优化算法时，我们需要为变量θ选取一些初始值。对于高级优化算法，它默认你会为变量θ提供一些初始值。对于梯度下降算法，同样地，我们也需要对θ进行初始化，初始化完毕以后，我们就可以一步一步通过梯度下降来最小化代价函数J(θ)。
有一种初始化θ的想法是将θ的初始值全部设为0，尽管在逻辑回归中这样做时被允许的，但实际上在训练网络时，将所有参数初始化为0起不到任何作用。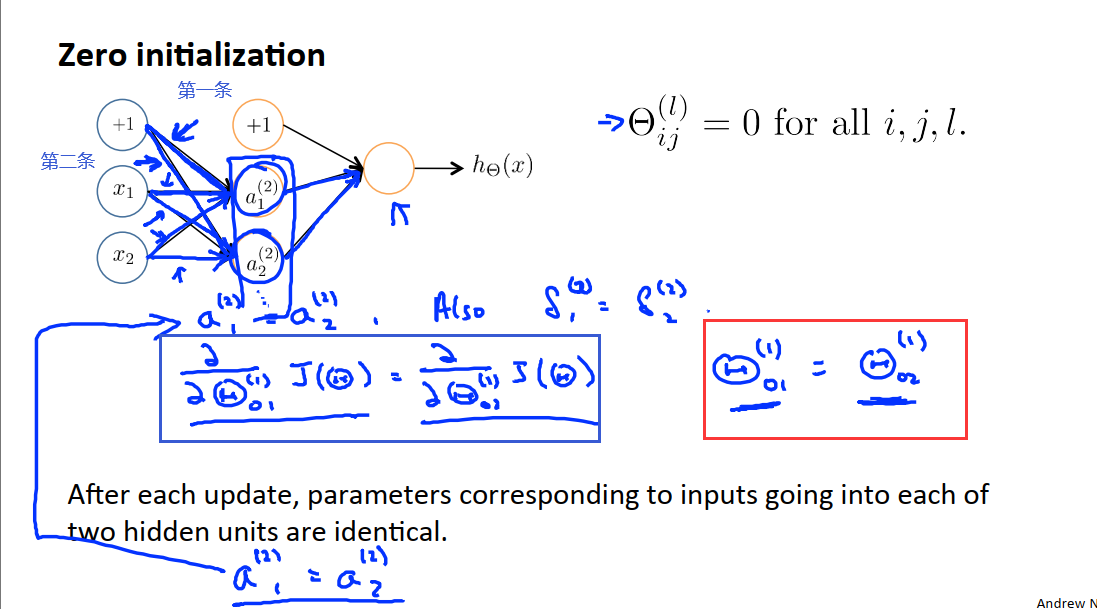

以上图这个神经网络的训练为例，假如我们将网络中所有参数初始化为0，这样的话，就意味着在这个例子中，蓝色边的权重全部为0.隐藏单元a1和a2都是以同一输入函数来计算的。于是对于神经网络中所有的训练样本最后总能得到a^2_1 = a^2_2。犹豫这些权重都是相等的，就可以得出这些δ值也都相同，具体来说会得到δ^2_1 = δ^2_2。然后我们就会发现，代价函数J(θ)关于θ的偏导数会满足上图中蓝框内的条件。这意味着即使每一次的梯度下降更新中第一条蓝色的权重会被更新为学习率乘等式左边的式子，第二条蓝色的权重会被更新为学习率乘右边这个式子，但这就意味着当对这两条蓝色的权重进行梯度下降更新，最后上图中红框内的参数将会相等，虽然现在它们都不为0了。同样地，就算再进行一次梯度下降，红框内这两个参数值依然相等。
所以每次更新之后，这两个隐藏单元的每个参数输入都是相等的，也就是说，第一条和第二条权重依然相等，第三条和第四条权重依然相等、第五条和第六条权重依然相等。这意味着即使梯度下降进行了一次迭代，但这两个隐藏单元依然以相同的函数来计算输入对应的输出。所有的隐藏单元都在计算相同的特征，这是一种高度冗余的现象，这意味着最后的逻辑回归单元只能得到一个特征。
为了解决这一问题(对称权重问题，也就是所有神经元的输入的权重都是一样的)，在神经网络中对参数进行初始化时，要使用随机初始化的思想。因此对每一个θ值，w偶们将其初始化为一个范围在-epsilon到epsilon之间的随机值。我们使用的方法如下图：

总而言之，为了训练神经网络应首先要将权重随机初始化为一个接近0的，范围在-epsilon到epsilon之间的数，然后进行反向传播，再进行梯度检验，最后使用梯度下降或者其他高级优化算法来最小化代价函数J(θ)，为参数选取一个随机化随机初始化的值开始，这是一种打破对称性的流程。

16.13 组合到一起

本小节我们会了解到神经网络算法的总体实现过程。

16.13.1 确定神经网络架构

在训练一个神经网络时，我们要做的第一件事就是选择一种网络架构，这里的架构是指神经元之间的连接模式。如下图，我们可能会从以下几种架构中选择：
1 包含3个输入单元，5个隐藏单元和4个输出单元。
2 包含3个输入单元，两组5个隐藏单元和4个输出单元。
3 包含3个输入单元，三组5个隐藏单元和4个输出单元。
我们可以选择每一层有多少个隐藏单元以及有多少个隐藏层。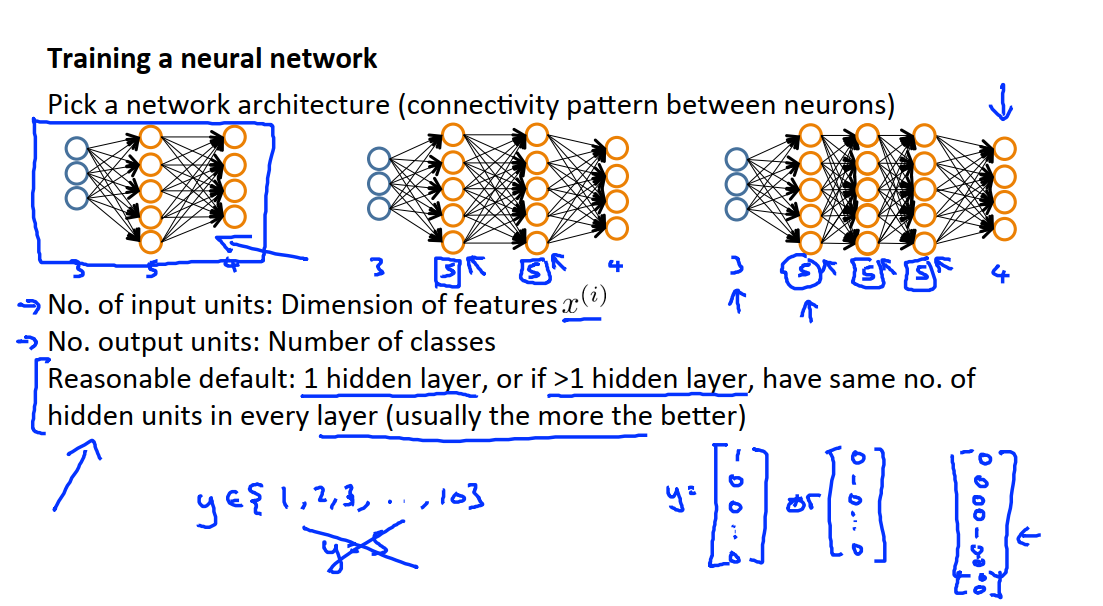

那么我们如何做出选择呢？
1 我们已经定义了输入单元的数量，一旦我们确定了特征集x，输入单元的数量就等于特征x^i的维度。
2 如果我们正在进行多类别分类，那么输出层的单元数目将会由分类问题中所要区分的类别个数确定。如果多元分类问题y的取值范围是在1到10之间，那么就有10个可能的分类，需要把输出y重写成向量的形式。
3 对于隐藏层单元的个数以及隐藏层的数目，一个合理的默认选项是只使用单个隐藏层，所以最左边所示的神经网络架构可能是最常见的；如果使用不止一个隐藏层，一个合理的默认选型，那就是每一个隐藏层通常都应有相同的单元数，通常情况下，隐藏单元越多越好。不过需要注意的是，如果有大量隐藏单元，计算量一般会比较大。
但实际上来说，上图中左边第一个结构更为常用。
一般来说，每个隐藏层所包含的单元数量还应该和输入的x维度相匹配，即和特征的数目相匹配，隐藏单元的数目可以和输入特征的数量相同或者是它的二倍、或者三倍。

16.13.2 训练神经网络

1 随机初始化权重。通常我们把权重初始化为很小的值，接近于零。
2 实现前向传播算法。也就是对于该神经网络任意输入一个x^i,计算出对应的h(x)值，也就是一个输出向量y。
3 实现代价函数J(θ)。
4 实现反向传播算法来算出J(θ)关于参数θ的偏导数。具体来说，实现反向传播，我们要对所有训练样本使用一个for循环进行遍历，可能有相当先进的向量化方法不需要使用for循环对m个训练样本进行遍历，但是第一次执行反向传播，可以使用一个for循环来完成程序。在for循环中，我们对这个样本执行前向传播和反向传播算法，然后我们就能得到神经网络每一层中每一个单元对应的激励值和δ项。然后在循环内部我们计算出这些Δ项的值，然后在循环外部，我们用这些值来计算出偏导数项。
5 使用梯度检查来确定已经计算得到的偏导数项是否正确。也就是把反向传播算法得到的偏导数值与用数值方法得到的估计值进行比较。在确定无误之后禁用梯度检查部分代码。
6 使用一个最优化算法比如梯度下降算法或更加高级的优化方法(LBFGS,共轭梯度法等等)，将这些方法与反向传播算法相结合，来最小化关于θ的代价函数J(θ)。理论上，这些算法理论上都可能收敛于局部最小值，但一般来讲，在实际操作中，它们都能够解决问题。

17 逻辑回归多分类实现

17.1 读取图片

我们要解决的问题是手写数字识别。在提供的原始数据中，y的取值为1-10，y=10表示当前数字为0。
读入.mat文件需要用到以下工具：
scipy：是一个高级的科学计算库，它和Numpy联系很密切。scipy一般都是操控numpy数组来进行科学计算。scipy有很多子模块可以应对不同的应用，例如插值运算，优化算法，图像处理，数学统计等。
scipy.io:数据输入输出相关模块。
loadmat:读入.mat文件的方法。
实现代码如下：

import numpy as np
import matplotlib.pyplot as plt
import scipy.io as sio

# 返回的data是一个字典格式
data = sio.loadmat('ex3data1.mat')
type(data)
# 打印字典的key,可以发现数据集的名字为X和y
data.keys()

raw_X = data['X']
raw_y = data['y']
print(raw_X.shape,raw_y.shape)
# 400实际上是把一个图像向量化的结果，真实的维度是20*20

# 定义一个用来打印图片的函数
def plot_an_image(X):
    random_one = np.random.randint(5000)
    # 取第random_one行的所有元素
    image = X[random_one,:]
    # 定义取出图片的大小
    fig,ax = plt.subplots(figsize=(1,1))
    # 显示图片,必须把图片从向量还原成矩阵,并设置白底灰字
    ax.imshow(image.reshape(20,20).T,cmap='gray_r')
    # 去掉刻度
    plt.xticks([])
    plt.yticks([])

# 打印图片
plot_an_image(raw_X)

17.2 损失函数&梯度向量

我们在最小化代价函数的时候使用高级优化方法，例如scipy.optimize.minimize,它的主要参数有：
fun：要优化的函数。
method：优化方法，这里我们使用的为method=’TNC’,全称为truncated newton algorithm。
jac：梯度向量
x0：θ参数初始值，需要进行向量化
arg：X，y和正则化项的λ

向量(n,)和数组(n,1)在矩阵相乘时的区别：
第一类： np.dot(A,B),np.matmul(a,b),a@b
1.1 对于二维矩阵，矩阵乘积。
1.2 对于 一维矩阵，内积，结果是一个数值。
第二类： np.multiply(A,B)或*,表示对应元素相乘，数量积，结果的维度没有任何改变。

定义激活函数

def sigmoid(z):
    return 1/(1+np.exp(-z))

定义costFunction

# 注意costFunction中参数的顺序,传入的θ是一维数组
# 注意costFunction中参数的顺序,传入的θ是一维数组
def costFunction(theta,X,y,lamda):
    inner = sigmoid(X@theta)
    first = y*np.log(inner)
    second = (1-y)*np.log(1-inner)
    # 利用向量内积计算平方和
    reg = theta[1:]@theta[1:]*(lamda/(2*len(X)))
    return -np.sum(first+second)/len(X)+reg

定义计算梯度的函数

# 注意计算梯度向量的函数参数的顺序
def gradient_reg(theta,X,y,lamda):
    # 带有正则化项的偏导数，j=1时开始加正则项的导数
    reg = theta[1:]*lamda/len(X)
    # 因为我们不对θ0进行任何操作，所以我们在reg第一行之前插入一行0
    # 插入对象为reg，位置是在第一行，值为0，对所有列操作所以axis=0
    reg = np.insert(reg,0,values=0,axis=0)
    first = (X.T@(sigmoid(X@theta)-y))/len(X)
    return first+reg

数据集准备

# 在数据raw_X,最前面(0)加上全为1(values)的一列,axis为对所有列操作
X = np.insert(raw_X,0,values=1,axis=1)
X.shape
# y向量化
y = raw_y.flatten()
y.shape

17.3 多分类器设计、优化

输入数据的维度是401，0-9共是10个数字，也就是我们需要10个逻辑分类器，那么总共的参数为10*401，我们把参数放在一个二维数组中。

from scipy.optimize import minimize
# 参数K为标签个数
def one_vs_all(X,y,lamda,K):
    # 获取输入数据的维度(第二个参数)，这里为401
    n = X.shape[1]
    theta_all = np.zeros((K,n))
    # 10个分类器依次预测,从1-10
    for i in range(1,K+1):
        # 每一个分类器的θ是一个向量
        theta_i = np.zeros(n,)
        # args参数首先传入X，然后是当前分类器要判别的标签，最后是λ
        res = minimize(fun=costFunction,x0=theta_i,args=(X,y==i,lamda),method='TNC',jac=gradient_reg)
        # 把得到的最优参数写回到θ_all
        theta_all[i-1,:] = res.x
    return theta_all

lamda = 1
K = 10
theta_final = one_vs_all(X,y,lamda,K)
print(theta_final)

17.4 预测

def predict(X,theta_final):
    # X是5000*401，theta_final是10*401，h是5000*10，也就是10个分类器对500个输入分别进行了预测
    h = sigmoid(X@theta_final.T)
    # 寻找概率最大的那一个分类器的索引,axis=1是对所有行操作
    h_argmax = np.argmax(h,axis=1)
    # 索引和标签差1
    return h_argmax+1
y_pre = predict(X,theta_final)
acc = np.mean(y_pre==y)
print(acc)

18 神经网络多分类实现

18.1 加载训练好的模型

相关概念与符号如下图：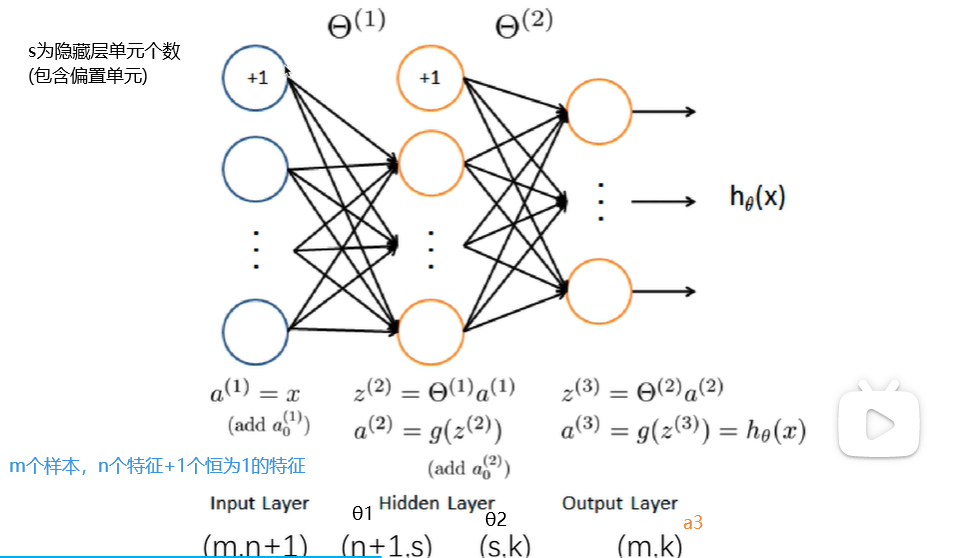

我们用神经网络实现手写数字识别。

import numpy as np
import scipy.io as sio
data = sio.loadmat('ex3data1.mat')
raw_X = data['X']
raw_y = data['y']
X = np.insert(raw_X,0,values=1,axis=1)
X.shape

# 便于计算准确率
y = raw_y.flatten()
y.shape

# 读入参数
theta = sio.loadmat('ex3weights.mat')
theta.keys()

# 从输入层到隐藏层
theta1 = theta['Theta1']
# 从隐藏层到输出层
theta2 = theta['Theta2']
theta1.shape,theta2.shape

def sigmoid(z):
    return 1/(1+np.exp(-z))

# 第一层输入特征
a1 = X
z2 = X@theta1.T
a2 = sigmoid(z2)
a2.shape

z3 = a2@theta2.T
a3 = sigmoid(z3)
a3.shape

# a3按行寻找最大的概率，作为预测的结果
y_pre = np.argmax(a3,axis=1)
y_pre = y_pre+1
acc = np.mean(y_pre==y)
print(acc)

18.2 独热编码

为了训练神经网络，我们需要对y做变换，即one-hot编码。将y表示为一个k维的向量，只有label对应的位为1，其余都是0。

import numpy as np
import scipy.io as sio
import matplotlib.pyplot as plt
from scipy.optimize import minimize
data = sio.loadmat('ex4data1.mat')
raw_X = data['X']
raw_y = data['y']
X = np.insert(raw_X,0,values=1,axis=1)
X.shape

def one_hot_encoder(raw_y):
    # 用于存放编码结果
    result = []
    # 循环编码每一个label
    # raw_y的值是1-10，但是向量索引从0开始
    for i in raw_y:
        y_temp = np.zeros(10)
        y_temp[i-1] = 1
        result.append(y_temp)
    # 返回值转换成数组
    return np.array(result)

y = one_hot_encoder(raw_y)
print(y)
y.shape

18.3 序列化权重参数

theta = sio.loadmat('ex4weights.mat')
theta1,theta2 = theta['Theta1'],theta['Theta2']
theta1.shape,theta2.shape

def serialize(a,b):
    return np.append(a.flatten(),b.flatten())

theta_serialize = serialize(theta1,theta2)
theta_serialize.shape

18.4 解序列化

def deserialize(theta_serialize):
    # :表示从头开始
    theta1 = theta_serialize[:25*401].reshape(25,401)
    # ：表示到结束
    theta2 = theta_serialize[25*401:].reshape(10,26)
    return theta1,theta2

theta1m,theta2 = deserialize(theta_serialize)
theta1.shape,theta2.shape

def sigmoid(z):
    return 1/(1+np.exp(-z))

def feed_forward(theta_serialize,X):
    theta1,theta2 = deserialize(theta_serialize)
    a1 = X
    z2 = a1@theta1.T
    a2 = sigmoid(z2)
    # 5000*25->5000*26，对每一行操作
    a2 = np.insert(a2,0,values=1,axis=1)
    z3 = a2@theta2.T
    a3 = sigmoid(z3)
    # 后面反向传播需要用到
    return a1,z2,a2,z3,a3

18.5 损失函数

损失函数的计算方法如下图，分有正则化项和无正则化项两种情况：

# 不带正则化的损失函数
def cost(theta_serialize,X,y):
    a1,z2,a2,z3,h = feed_forward(theta_serialize,X)
    J = -np.sum(y*np.log(h)+(1-y)*np.log(1-h))/len(X)
    return J

# 带正则化的损失函数
def reg_cost(theta_serialize,X,y,lamda):
    a1,z2,a2,z3,h = feed_forward(theta_serialize,X)
    theta1,theta2 = deserialize(theta_serialize)
    # 先计算theta1的平方和
    sum1 = np.sum(np.power(theta1[:,1:],2))
    sum2 = np.sum(np.power(theta2[:,1:],2))
    reg = (sum1+sum2)*lamda/(2*len(X))
    return reg+cost(theta_serialize,X,y)

18.6 梯度

梯度计算的依据：

需要添加的正则化项：

# 无正则化项
def gradient(theta_serialize,X,y):
    # 解序列化
    theta1,theta2 = deserialize(theta_serialize)
    # 前向传播
    a1,z2,a2,z3,h = feed_forward(theta_serialize,X)
    d3 = h-y
    #d3是5000*10维，theta2是10*26维的，z2是5000*25维的，
    d2 = d3@theta2[:,1:].T*sigmoid_gradient(z2)
    # 10*5000 5000*25 = 10*25 16.8节有对应公式
    D2 = (d3.T@a2)/len(X)
    D1 = (d2.T@a1)/len(X)
    return serialize(D1,D2)

# 带有正则化项
def reg_gradient(theta_serialize,X,y,lamda):
    D = gradient(theta_serialize,X,y)
    D1,D2 = deserialize(D)
    theta1,theta2 = deserialize(theta_serialize)
    # 偏置项不参与正则化
    D1[:,1:] = D1[:,1:] + theta1[:,1:]*lamda/len(X)
    D2[:,1:] = D2[:,1:] + theta2[:,1:]*lamda/len(X)
    return serialize(D1,D2)

18.7 优化

 def nn_training(X,y):
    # 范围为-0.5到0.5，个数为10285
    init_theta = np.random.uniform(-0.5,0.5,10285)
    # options的maxiter设置的是最大迭代次数
    # res = minimize(fun=cost,x0=init_theta,args=(X,y),method='TNC',jac=gradient,options={'maxiter':300})
    res = minimize(fun=reg_cost,x0=init_theta,args=(X,y,lamda),method='TNC',jac=reg_gradient,options={'maxiter':300})
    return res

lamda = 10
res = nn_training(X,y)
raw_y = data['y'].reshape(5000,)
_,_,_,_,h = feed_forward(res.x,X)
# 对每一行操作
y_pred = np.argmax(h,axis=1)+1
acc = np.mean(y_pred==raw_y)
print(acc)

18.8 隐藏层可视化

def plot_hidden_layer(theta):
    theta1,_ = deserialize(theta)
    # 去掉theta1中的第一列 25*400 我们可以看成是5*5的样本，每个样本含有20*20个数据
    hidden_layer = theta1[:,1:]
    fig,ax = plt.subplots(ncols=5,nrows=5,figsize=(8,8),sharex=True,sharey=True)
    for r in range(5):
        for c in range(5):
            ax[r,c].imshow(hidden_layer[5*r+c].reshape(20,20).T,cmap='gray_r')
    plt.xticks([])
    plt.yticks([])
    plt.show

plot_hidden_layer(res.x)

19 使用机器学习的建议

19.1 机器学习诊断法

在房价预测中，假如我已经完成了正则化线性回归，也就是最小化代价函数J的值。在学习到参数之后，如果我将假设函数放到一组新的房屋样本上进行测试，假如我在预测房价时产生了巨大的误差，那么要想要改进这个算法，我们的方法有：
1 使用更多的训练样本。例如通过电话调查或上门调查来获取更多的不同的房屋出售数据。
2 尝试选用更少的特征集。
3 尝试选用更多的特征。
4 尝试添加多项式特征。例如x1^2,x2^2等等。
5 尝试减小λ。
6 尝试增大λ。

机器学习诊断法：这是一种测试方法，我们可以通过这种测试来了解算法在哪里出了问题，这通常也能帮助我们改进一种算法的效果，要采用什么样的尝试才是有意义的。
这些诊断法的执行和实现是需要花费时间的，但这样做的确是把时间用在了刀刃上。因为诊断法能帮助我们更早发现某些方式是无效的。

19.2 评估假设函数

当我们确定学习算法的参数时，我们考虑的是选择参数来使训练误差最小化。但是并不是训练误差越小越好，这会使得模型很难泛化到新的数据集上。因此我们需要一个新的评价假设函数的方法。
我们将所有数据分成训练集和测试集，其中一种典型的分割方法是按照7：3的比例，将70%的数据作为训练集(m表示训练样本的总数)，30%的数据作为测试集(m_test表示测试样本的总数，下标test表示这些样本是来自测试集)，但如果这组数据有某种规律或顺序的话，那么最好是随机选择，如果数据已经随机分布了，那么就可以选择前70%和后30%。
训练和测试闲心回归的方法：
1 首先需要对训练集进行学习得到参数θ，具体的方法就是使用70%的训练样本最小化训练误差J(θ)
2 使用学习得到的θ计算训练集上的误差J_test。具体计算方式如下图，为平方误差的计算方式(和线性回归的J(θ)计算方式一致)

训练和测试逻辑回归的方法：
1 从数据集中70%的训练数据中得到了参数θ。
2 使用学习得到的θ计算训练集上的误差J_test。具体计算方式如下图，为逻辑回归中J(θ)的计算方式。
3 也可以使用另一种方式定义分类，误差0/1分类错误度量：如果预测结果和数据的label一致，则error值不变，否则error值加1。最终test_error的值就是error/m_test。

19.3 模型选择和训练、验证、测试集

我们已经多次接触到了过拟合问题了，即使模型对训练数据拟合很好，假设函数也可能存在不能很好的泛化到新的数据集的问题，所以不能用来判断假设函数的好坏。
我们现在要选择能最好地拟合数据的多项式次数，例如一次函数、二次函数等等一直到十次函数中的哪一个。我们在算法中增加一个参数d表示应该选择的多项式次数，所以除了参数θ，还有一个参数d，都需要用数据集来决定。

上图中，首先我们选择d=1的模型，然后最小化训练误差，得到参数向量θ^1。然后我们继续选择d=2的模型，然后最小化训练误差，得到参数向量θ^2。然后我们对每一个模型求出测试集误差，从这些模型中选出最好的一个，我们的标准是哪个模型有最小的测试误差。
在上图的例子中，我们最终选择了五次多项式模型，但是要注意测试集误差并不能很好地评估出这个假设函数的泛化能力，原因是我们拟合了一个额外的参数d，也就是多项式的次数，也就是我们选择了一个能最好地拟合测试集的参数d的模型。我们用测试集拟合得到的参数d，再在测试集上评估假设函数就不公平了。
如果我们用训练集来拟合参数θ0、θ1等等，那么拟合后的模型在训练集上的效果是不能预测出假设函数对于新样本的泛化能力的。同理，我们在测试集来拟合参数d，那么拟合后的模型在测试集上的效果是不能预测出假设函数对于新样本的泛化能力的。
为了解决这个问题，我们通常会把数据集分成三个部分，训练集、交叉验证(cross validation,cv,验证集)和测试集。这些数据的分配比例是60%、20%、20%。训练集的数量为m，验证集的数量为m_{cv},测试集的数量为m_{test}。
与训练集、验证集、测试集相对应的是训练误差、验证误差和测试误差，具体计算方式如下图。

当面对模型选择问题时，我们要做的是用验证集来选择模型。例如，我们选择第一个模型，然后使用训练集最小化代价函数，得到模型的参数向量θ^1,然后对后面的模型采用类似的操作。然后我们使用验证集来测试每一个模型并计算出对应的J_cv,然后选择J_cv最小的假设函数作为我们的模型。我们假设四次多项式对应的交叉验证误差最小，因此我们将选择它作为我们的模型，也就是参数d=4。我们可以用测试集来评估算法选出的模型的泛化误差。

19.4 诊断偏差与方差

当我们运行一个算法时，如果这个算法的表现不理想，那么多半时出现两种情况，要么是偏差比较大，要么是方差比较大，即要么是欠拟合问题，要么是过拟合问题。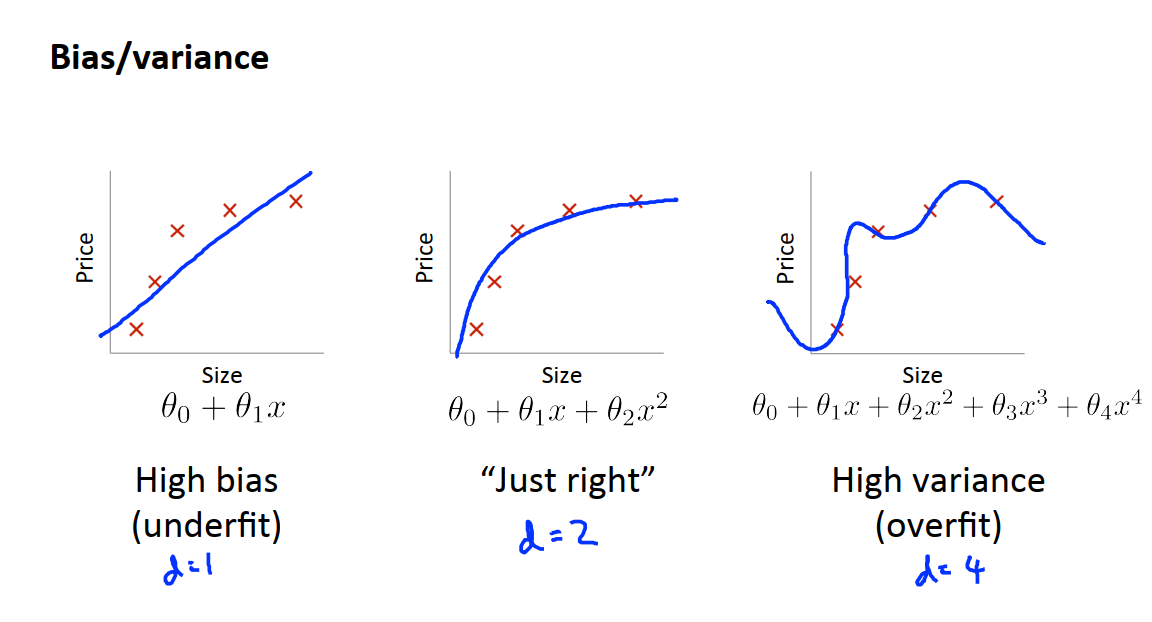

如果用简单的假设函数来拟合数据，如上图中的左一，那么就会欠拟合；而如果用很复杂的假设来拟合时如上图中的右一，那么就会过拟合；只有采用中等复杂度的假设，比如某种二次多项式的假设，对数据拟合得刚刚好，如上图中的右二，泛化误差也是三种情况中最小的。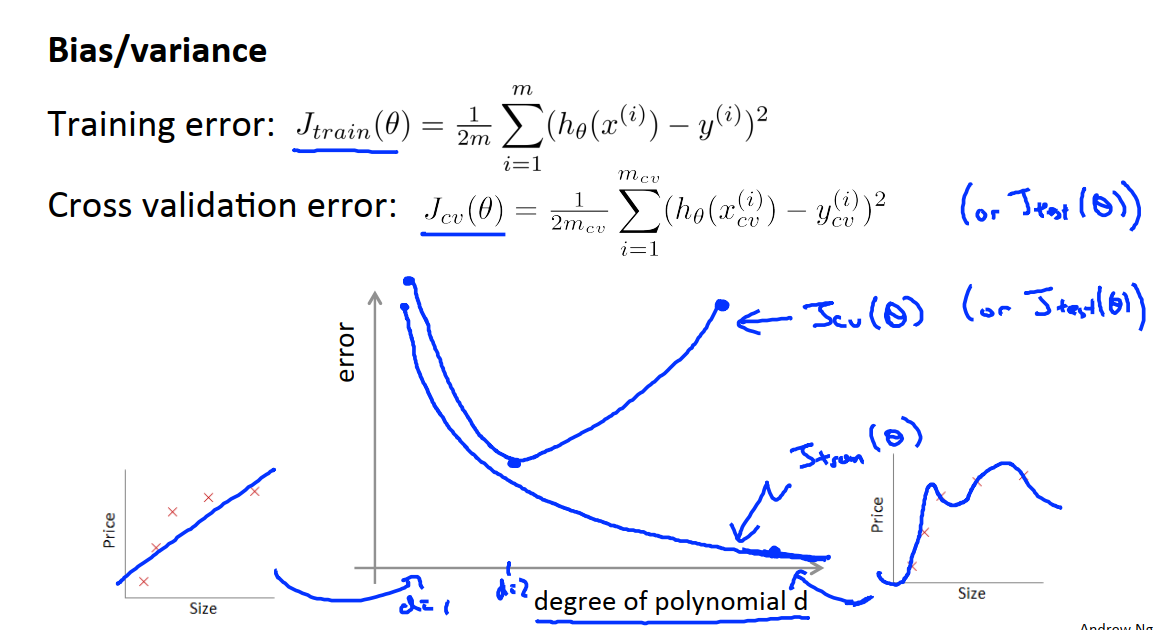

在上图中，横坐标表示多项式的次数，因此横坐标越往右的位置表示多项式的次数越大，左一的d较小，对应更高的训练误差，右一的图d较大表示更复杂的函数，更高的阶数，我们对训练集的拟合程度越来越好，对应更小的训练误差，具体函数图像如上图中的J_train。
验证集上的误差与多项式的次数关系如上图中的J_cv。而且J_test可能也会得到一条类似的曲线。

假设我得出了一个学习算法，但是这个算法并没有表现地像我期望的那么好，如果我的交叉验证误差或者测试集误差都很大，根据上图我们判断，此时的d位于图中的靠左边或是靠右边，靠左边对应的就是高偏差的问题，也就是我们的多项式次数过低；靠右边对应的就是高方差的问题，也就是我们的多项式次数过高。上图也提示了我们如何区分这两种情况。
对于高偏差的情况，也就是对应欠拟合的情况，我们发现交叉验证误差和训练误差都会很大。
对于高方差的情况，也就是对应过拟合的情况，我们发现交叉验证误差高(远大于训练误差)但是训练误差很小。

19.5 正则化和偏差、方差

探讨偏差、方差和算法的正则化之间的关系，正则化时如何影响偏差和方差的。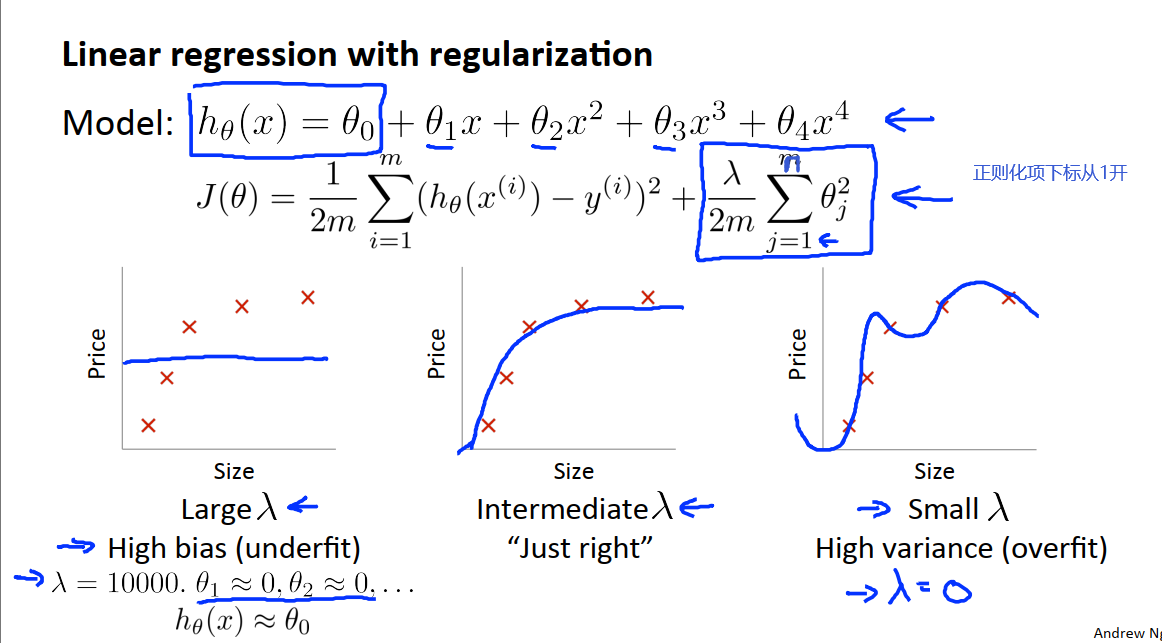

如上图左一，当正则化参数非常大时，此时除了θ0外的θ参数将被惩罚很重，其结果是这些参数大部分都接近于0，并且这个假设函数h(x)将等于或者近似等于θ0。因此我们最终得到的假设函数如左一所示，是近似水平的一条直线，因此这个假设处于高偏差，对数据集严重欠拟合。
如上图右一，当正则化参数非常小时，在这种情况下我们要拟合一个高阶多项式的话，通常会出现过拟合的情况，因此这个假设处于高方差。
在选择正则化参数时，我们的训练误差、验证误差和测试误差都定义为平方和误差，而不使用正则化项，具体如下图：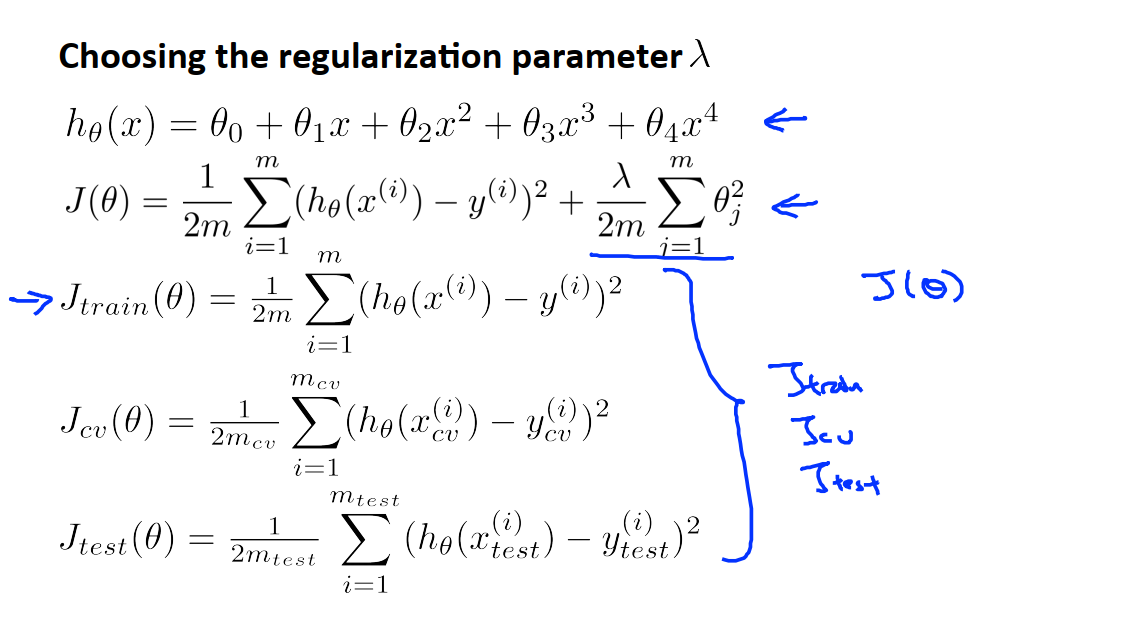

具体的过程是选取一系列想要尝试的λ值，可以以2倍的比例增长，首先考虑不使用正则化，即λ=0。例如，在λ=0时最小化代价函数J(θ)，得到一组参数θ^1。与此类似，我们对其余λ取值依次使用这种计算方法。
接着，我们使用交叉验证集对上述模型依次进行评估，然后将交叉验证误差最小的模型作为我们最终的选择。例如我们选择了θ^5,然后我们可以使用θ^5对应的模型来得到测试误差。如下图，注意J(θ)有正则化项，但是Jcv，Jtest都没有正则化项。

当正则化参数λ很小，也就是我们几乎没有使用正则化，因此很大可能处于过拟合；而当正则化参数λ很大时，我们很有可能处于高偏差的问题。从下图中我们可以看出，会有一个点，训练误差和验证误差都比较小，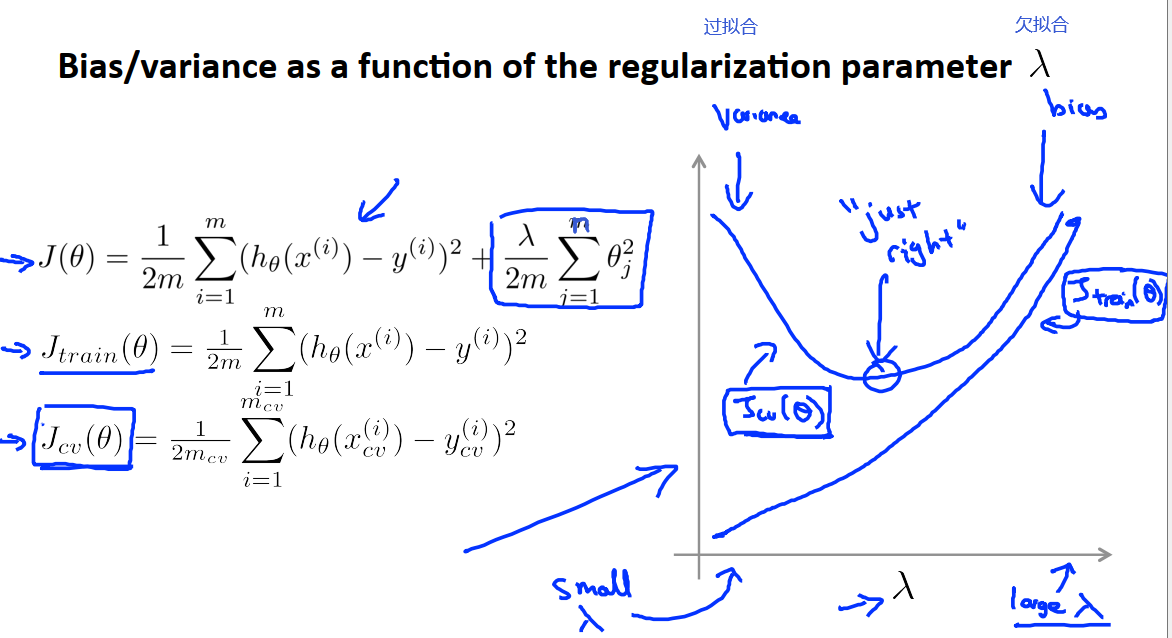

19.6 学习曲线

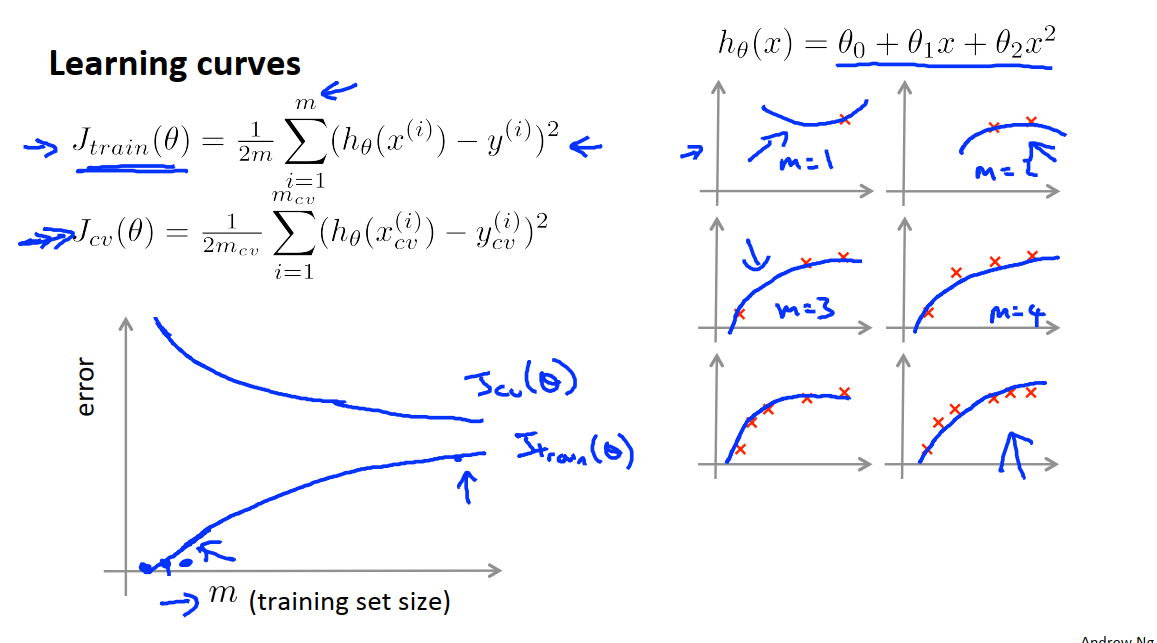
上图描述的是当我们使用二次函数来拟合不同样本个数的数据时，他的Jtrain和Jcv的变化趋势。在右图中，当只有1个样本点时，Jtrain=0，Jcv会比较大。当我们有2个样本点时，二次函数依然可以很好地拟合。当我们有3个样本点时，二次函数依然可以很好地拟合。这三种情况下如果我们不使用正则化，Jtrain就会等于0，如果我们使用正则化，Jtrain就会稍大于0。需要说明的是，如果我的训练集很大，我通过限制参与学习的样本数来绘制上面的关系图，那么在计算Jtrain时也只有参与学习的点参与计算，其他没有参与学习的样本也不参与Jtrain计算。
我们知道，当m很小时，训练集能够被很好地拟合，Jtrain也会很小；当训练集m越来越大的时候，使用二次函数拟合越来越困难了，Jtrain不断增大。
当训练集很小的时候，泛化程度不会很好，Jcv会比较大；当训练集比较大的时候，才有可能得到一个比较合适的假设函数，Jcv和Jtest都会随着训练样本容量m的增加而减小。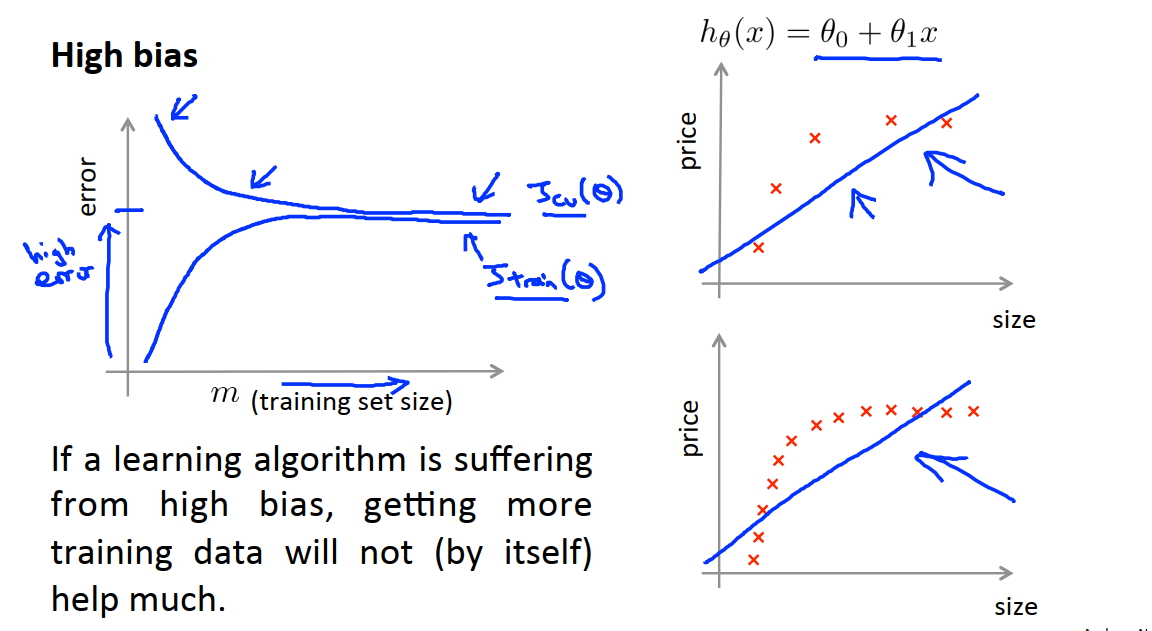

上图中，如果假设函数出现高偏差问题，例如我们用一条直线来拟合数据。那么对于这个假设函数，随着样本数m的增多，交叉验证误差有略微的下降，但是当他到达一个较优的点时，随着数据集样本数量的增多，Jcv不再变化。
当m比较小时，训练误差是比较小的，随着m的增大，Jtrain逐渐增大直到接近交叉验证误差。这是因为模型的参数很少，我们又有很多的数据，当m很大的时候，训练集和交叉验证集的误差将会非常接近。所以高偏差也就是欠拟合的特点是高训练误差和高交叉验证误差。这也说明了如果一个学习算法有高偏差，获得更多的训练样本对于改善算法的表现没有帮助。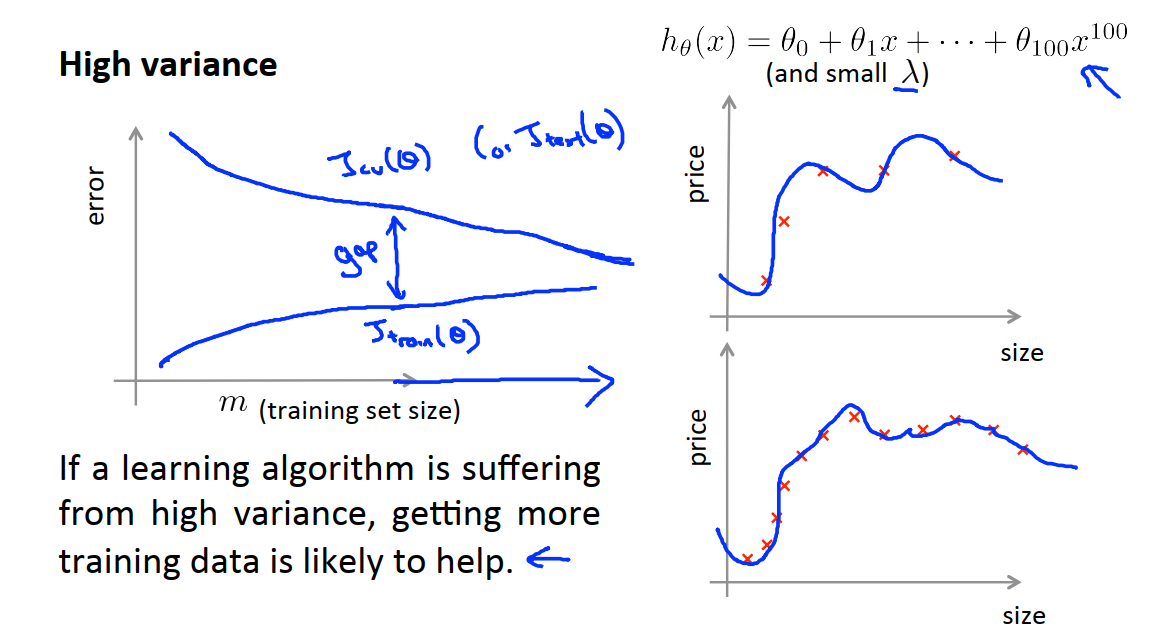

如上图，当学习算法正出现高方差时的情况。当训练样本数m比较小的时候，如果此时的正则化项λ也比较小，那么我们得到的假设函数就会把数据集拟合的很好，此时Jtrain就会很小，随着训练集样本容量的增加，可能也会过拟合，但此时要对数据很好地拟合变得更加困难了，Jtrain的值也随之增加。
在高方差情况下，假设函数对数据过拟合，因此Jcv一直都很大，因此过拟合的特点是Jcv和Jrain相差比较大。这也说明了如果一个学习算法有高方差，获得更多的训练样本对于改善算法的表现有帮助。

19.7 总结

在19.1中我们提供了一些改进算法的方法，现在我们进一步讨论它们适用的问题：
1 使用更多的训练样本。->解决高方差问题。->交叉验证误差大于训练集误差。
2 尝试选用更少的特征集。->解决高方差问题。
3 尝试选用更多的特征。->解决高偏差问题。->现有的假设函数过于简单。
4 尝试添加多项式特征。->解决高偏差问题。->类似于增加特征。
5 尝试减小λ。->解决高偏差问题。
6 尝试增大λ。->解决高方差问题。
为神经网络模型选择结构或连接形式的经验。当我们在进行神经网络拟合的时候，我们可以选择一个相对比较简单的神经网络模型，隐含单元比较少，甚至只有一个隐含单元，像这样的神经网络参数就不会很多，容易出现欠拟合，下面左图中这种比较小型的神经网络最大的优势在于计算量较小。与之相对的另一种情况是拟合较大型的神经网络结构，如下面右图，每一层中的隐含单元数很多，或者有很多个隐含层，这种比较复杂的神经网络，参数一般较多，更容易出现过拟合，同时，这种结构会有很大的计算量。事实上，越大型的神经网络性能越好，但如果发生了过拟合，我们可以使用正则化方法来修正，这样最终的效果通常比使用一个小型的神经网络效果更好。最终，我们需要选择需要的隐含层的层数，选择的方法和λ的确定方法类似，把数据集分割为训练集、验证集和测试集。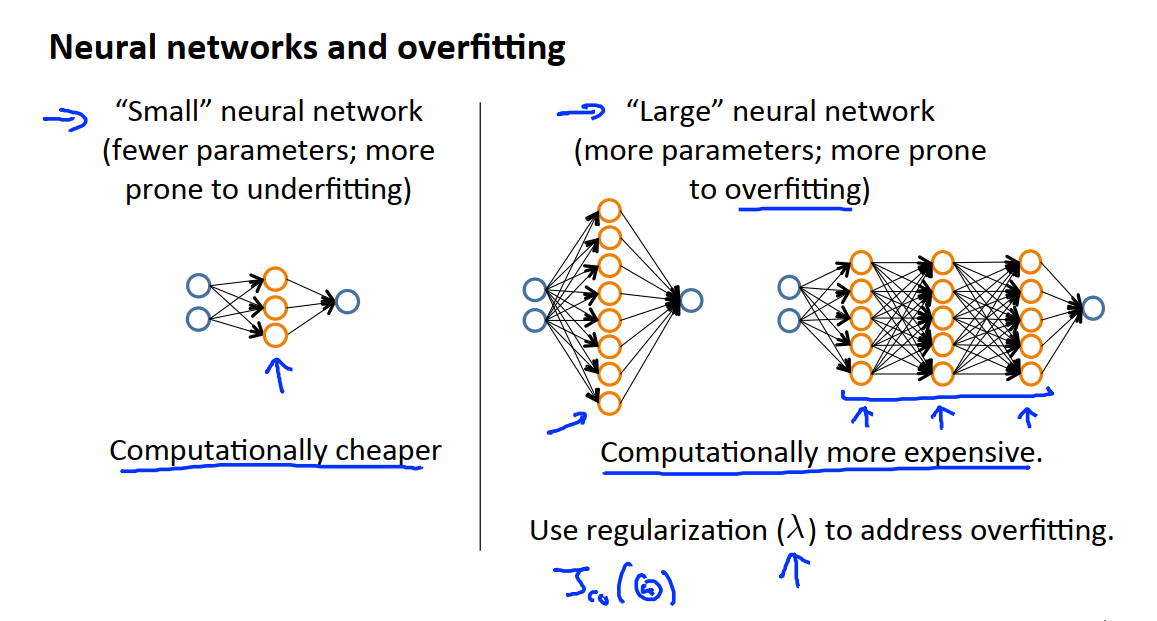

20 偏差和方差实战

20.1 数据导入、可视化、损失函数

偏差：预测值与真实值的差距，表示算法本身的拟合能力。
方差：预测值的变化范围，表示数据扰动所造成的影响。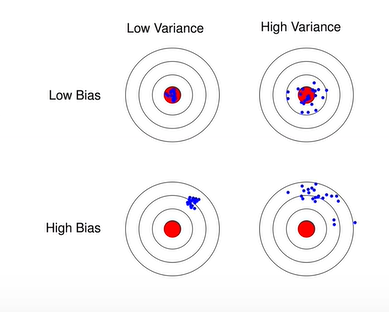

训练集：训练模型。
验证集：模型选择，模型的最终优化。
测试集：利用训练好的模型测试其泛化能力。
我们的任务是利用水库水位变化预测大坝出水量。
线性回归中的损失函数和梯度的计算方法如下：

数据导入代码：

import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat
from scipy.optimize import minimize
data = loadmat('ex5data1.mat')
data.keys()

# 训练集
X_train,y_train = data['X'],data['y']
X_train.shape,y_train.shape

# 验证集
X_val,y_val = data['Xval'],data['yval']
X_val.shape,y_val.shape

# 测试集
X_test,y_test = data['Xtest'],data['ytest']
X_test.shape,y_test.shape

# 插入第一列的1
X_train = np.insert(X_train,0,values=1,axis=1)
X_val = np.insert(X_val,0,values=1,axis=1)
X_test = np.insert(X_test,0,values=1,axis=1)

数据可视化代码：

def plot_data():
    fig,ax = plt.subplots()
    # 插入的那一列胡参与画图
    ax.scatter(X_train[:,1],y_train)
    ax.set(xlabel='change in water level(x)',ylabel='water flowing out og the dam(y)')

plot_data()

损失函数代码：

def reg_cost(theta,X,y,lamda):
    # theta是一维数组的形式
    cost = np.sum(np.power((X@theta-y.flatten()),2))
    reg = theta[1:]@theta[1:]*lamda
    return (cost+reg)/(2*len(X))

# 测试cost函数的正确性，theta向量的长度为训练集数据的第二个维度
theta = np.ones(X_train.shape[1])
lamda = 1
print(reg_cost(theta,X_train,y_train,lamda))

20.2 梯度&优化

梯度计算代码：

def reg_gradient(theta,X,y,lamda):
    # θ是向量的形式
    graf = (X@theta-y.flatten())@X
    reg = lamda*theta
    # 把θ0的reg项赋为0
    reg[0] = 0
    return (graf+reg)/len(X)

print(reg_gradient(theta,X_train,y_train,lamda))

模型训练代码：

def train_model(X,y,lamda):
    theta = np.ones(X.shape[1])
    res = minimize(fun=reg_cost,x0=theta,args=(X,y,lamda),method='TNC',jac=reg_gradient)
    return res.x

模型结果可视化：

theta_final = train_model(X_train,y_train,lamda=0)
# 数据集可视化结果
plot_data()
# 绘制回归结果
plt.plot(X_train[:,1],X_train@theta_final,c='r')
plt.show()

20.3 样本个数vs误差

绘制学习曲线：

def plot_learning_curve(X_train,y_train,X_val,y_val,lamda):
    # 创建一个列表用来存放训练样本的个数，为1-m个 +1是因为保证range取到len(X_train)
    x = range(1,len(X_train)+1)
    # 训练集损失函数
    train_cost=[]
    # 验证集损失函数
    cv_cost=[]
    for i in x:
        # x和y中的样本个数为i
        res = train_model(X_train[:i,:],y_train[:i,:],lamda)
        train_cost_i = reg_cost(res,X_train[:i,:],y_train[:i,:],lamda)
        # 在验证集上的样本数为全部
        cv_cost_j = reg_cost(res,X_val,y_val,lamda)
        train_cost.append(train_cost_i)
        cv_cost.append(cv_cost_j)
    # 训练集上的损失函数
    plt.plot(x,train_cost,label='training cost')
    plt.plot(x,cv_cost,label='cv cost')
    plt.legend()
    plt.xlabel('number of training examples')
    plt.ylabel('error')
    plt.show()

plot_learning_curve(X_train,y_train,X_val,y_val,lamda=0)

20.4 多项式特征&归一化

在上一步的学习曲线可视化之后，我们发现此时模型处于欠拟合状态，因此我们需要采用多项式特征来改善这一情况。
我们构造多项式特征的方法如下图：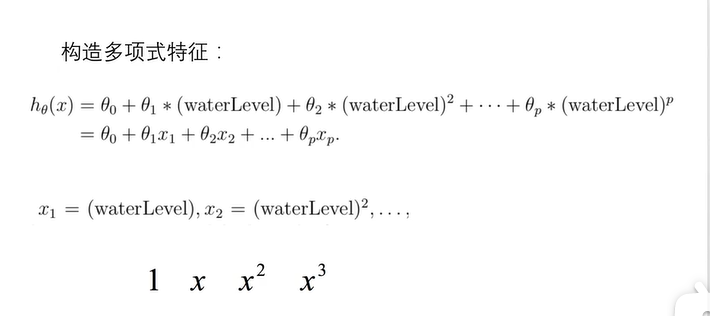

构造多项式特征的思路是每次在已有特征的基础上次数加一。
构造多项式代码：

def ploy_featrue(X,power):
    # 使用power+1可以保证i可以取到power
    for i in range(2,power+1):
        # 在x的最后一列插入X的i次方 X[:,1]是获取到X
        X = np.insert(X,X.shape[1],np.power(X[:,1],i),axis=1)
    return X

归一化代码：
学习进度

21 机器学习系统设计

学习进度